Kapitel
- Vollständige quadratische Gleichung
- Unvollständige quadratische Gleichungen
- Eigenschaften der Lösungen einer quadratischen Gleichung
- Quadratische Gleichung anhand ihrer Lösungen
- Faktorisierung eines Trinom 2. Grades
- Schritte für das Lösen von rationalen Gleichungen
- Biquadratische Gleichungen
- Schritte zum Lösen von irrationalen Gleichungen
- Gleichungen vom Grad größer als 2
Vollständige quadratische Gleichung
Die quadratische Gleichung lautet in ihrer vollständigen Form
mit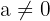 
. Die Lösung dieser Gleichung ist
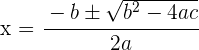
Unvollständige quadratische Gleichungen
Eine quadratische Gleichung ist unvollständig, wenn der Koeffizient 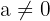und 
oder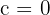 
Unvollständige Gleichung mit b = 0 und c = 0
In diesem Fall erfüllt der Wert 
die unvollständige Gleichung, weshalb die Lösung ist.
Unvollständige Gleichung mit c = 0
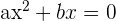
In diesem Fall faktorisieren wir die Gleichung und setzen gleich 0: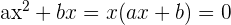 
Wir setzen die Faktoren gleich 0 und erhalten so die Lösungen 
und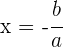 
Unvollständige Gleichung mit b = 0
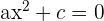
In diesem Fall sind die reellen Lösungen
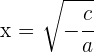und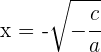 
,
immer wenn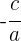 
positiv ist. Im Falle von negativ gibt es keine reellen Lösungen.
Eigenschaften der Lösungen einer quadratischen Gleichung
1Die Summe der Lösungen ist immer gleich dem Negativen des Quotienten von 
und 
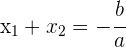
2Das Produkt der Lösungen ist gleich dem Quotienten von 
und
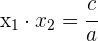
Quadratische Gleichung anhand ihrer Lösungen
Wenn man die Lösungen einer quadratischen Gleichung kennt, kann man die Gleichung aus ihnen ableiten. Dazu werden die Summe und das Produkt der Nullstellsten betrachtet.
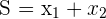
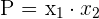
Die quadratische Gleichung, die die Lösungen 
und 
hat, ist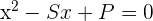 
Faktorisierung eines Trinom 2. Grades
Wenn die Nullstellen und der quadratischen Gleichung bekannt sind.
Die Gleichung wird wie folgt faktorisiert: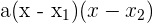 
Schritte für das Lösen von rationalen Gleichungen
1 Um sie zu lösen, werden die beiden Glieder der Gleichung mit dem kleinsten gemeinsamen Vielfachen der Nenner multipliziert.
2 Wir müssen die Lösungen überprüfen, um mögliche ungewöhnliche Lösungen auszuschließen, die aus der umgewandelten Gleichung stammen (die sich aus der Multiplikation mit dem kleinsten gemeinsamen Vielfachen ergibt), die aber nicht aus der ursprünglichen Gleichung stammen.
Biquadratische Gleichungen
Biquadratische Gleichungen haben die Form
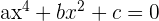
Zur Lösung substituieren wir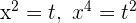 
; somit erhalten wir eine quadratische Gleichung mit der Unbekannten 
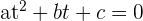
Für jeden positiven Wert von gibt es zwei Werte von 
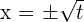
Wir können auch die Formel anwenden:
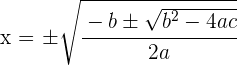
Schritte zum Lösen von irrationalen Gleichungen
1 Eine Wurzel wird in einem der beiden Glieder isoliert, wobei die übrigen Glieder, auch wenn sie ebenfalls Wurzeln enthalten, auf das andere Glied übertragen werden.
2 Wir quadrieren die beiden Glieder.
3 Wir lösen die erhaltende Gleichung.
4Es wird geprüft, ob die erhaltenen Lösungen die Ausgangsgleichung bestätigen. Wir müssen bedenken, dass die Quadrierung einer Gleichung eine andere Gleichung ergibt, die dieselben Lösungen wie die gegebene Gleichung hat und zusätzlich die Lösungen der Gleichung, die man erhält, wenn man das Vorzeichen eines der Glieder der Gleichung ändert.
5 Wenn die Gleichung mehrere Wurzeln enthält, werden die ersten beiden Arbeitsschritte wiederholt, bis alle Wurzeln eliminiert sind.
Gleichungen vom Grad größer als 2
Es handelt sich dabei um eine Gleichung beliebigen Grades der Form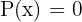 
. Das Polynom 
kann in Faktoren 1. und 2. Grades zerlegt werden. Es genügt dann, jeden der Faktoren gleich 0 zu setzen und die resultierenden Gleichungen 1. und 2. Grades zu lösen.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
