
Konzept der unvollständigen quadratischen Gleichung
ax² + bx + c = 0 (vollständige quadratische Gleichung)
Eine quadratische Gleichung ist unvollständig, wenn einer der Koeffizienten: b oder c oder beide gleich Null sind. Daher gibt es drei Fälle von unvollständigen quadratischen Gleichungen.
Erster Fall
Wenn beide Koeffizienten gleich Null sind, lautet die unvollständige quadratische Gleichung wie folgt:
Wenn b = 0 und c = 0 dann ist ax² = 0 (unvollständige quadratische Gleichung).
Für diese Art von Gleichung ist die Lösung immer x = 0.
Beispiele für unvollständige quadratische Gleichungen: Erster Fall
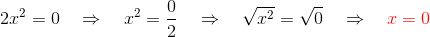
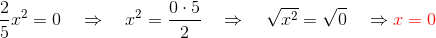
Zweiter Fall
Wenn der Koeffizient c gleich Null ist, lautet die unvollständige quadratische Gleichung wie folgt:
Wenn c=0 dann ist ax² + bx = 0 (unvollständige quadratische Gleichung).
So werden die Lösungen extrahiert:
1 Extrahiere den gemeinsamen Faktor x.
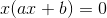
2 Da du ein Produkt gleich Null hast, ist entweder ein Faktor Null, oder der andere Faktor ist Null, oder beide sind Null.
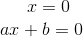
3 Daher sind die Lösungen:
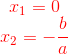
Beispiele für unvollständige quadratische Gleichungen: Zweiter Fall
1 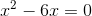
Nimm den gemeinsamen Faktor x heraus.
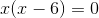
Da du ein Produkt gleich Null hast, setzte du die Faktoren gleich Null.
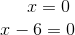
Die Lösungen sind:

2 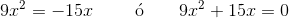
Nimm den gemeinsamen Faktor 3x heraus.
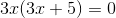
Setzte die Faktoren gleich Null, da du ein Produkt gleich Null hast.
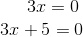
Die Lösungen sind:
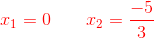
Dritter Fall
Wenn der Koeffizient b Null ist, lautet die unvollständige quadratische Gleichung wie folgt:
Wenn b = 0 dann ist ax² + c = 0 (unvollständige quadratische Gleichung).
So werden die Lösungen extrahiert:
1 Verschiebe den Term c in das zweite Glied mit wechselndem Vorzeichen.
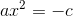
2 Übergebe den Koeffizienten a an das zweite Glied und dividiere
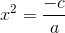
3 Die Quadratwurzel wird auf beiden Seiten der Gleichheit durchgeführt, und du erhältst zwei Lösungen, eine positive und eine negative, das heißt:
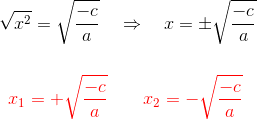
Beispiele für unvollständige quadratische Gleichungen: Dritter Fall
1 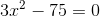
Übergebe den Term c an das zweite Glied mit wechselndem Vorzeichen.
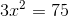
Übergebe den Koeffizienten a an das zweite Glied und dividiere.
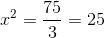
Die Quadratwurzel wird auf beiden Seiten der Gleichheit durchgeführt, und du erhältst zwei Lösungen, eine positive und eine negative, das heißt:
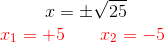
2 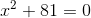
Übergebe den Term c an das zweite Glied mit wechselndem Vorzeichen.
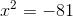
Übergebe den Koeffizienten a an das zweite Glied, das dividiert, aber da dies 1 ergibt, ist das Ergebnis das gleiche wie im vorherigen Schritt.
Wenn du beide Seiten der Gleichheit quadrierst, erhältst du einen negativen Radikanden, der keine Lösung in den reellen Zahlen hat.
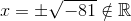
Mit KI zusammenfassen:













