Stelle die quadratische Gleichung mit den Lösungen 3 und -2 auf.
1 Da wir die Wurzeln der Gleichung kennen, können wir sie wie folgt beschreiben:
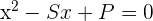
Wir benennen die Summe der Wurzeln mit  und das Produkt der Wurzeln mit
und das Produkt der Wurzeln mit 
2 Berechne  und
und 

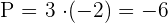
3 Die gesuchte quadratische Gleichung ist

Faktorisiere 
1 Löse die Aaufgabe, indem du die Formel für die Berechnung der Wurzel der quadratischen Gleichung anwendest:
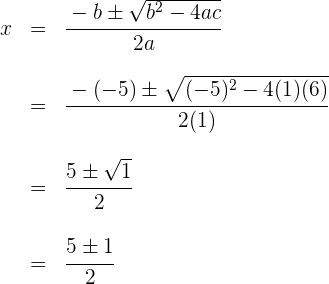
Die Wurzeln sind

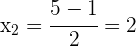
2 Anhand der Wurzeln kannst du nun wie folgt faktorisieren:
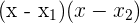
3 Die gesuchte Faktorisierung ist
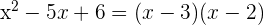
Ermittle den Wert k
für den Wert von  sind die Wurzeln in der Gleichung
sind die Wurzeln in der Gleichung 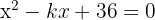 gleich.
gleich.
1 Damit beide Wurzeln gleich sind, muss ihr Diskriminante  gleich Null sein. Berechne die Diskriminante
gleich Null sein. Berechne die Diskriminante

2 Setze das Ergebnis gleich Null
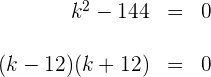
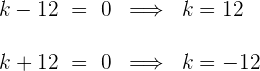
3 Setze jeden Faktor gleich Null und ermittle die Werte von  , für die die Wurzeln gleich sind:
, für die die Wurzeln gleich sind:
Die Summe von zwei Zahlen ist 5. Ihr Produkt ist −84. Finde die gesuchten Zahlen.
1 Wenn die Wurzeln der Gleichung bekannt wären, würde diese wie folgt aussehen:
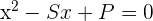
Die Summe der Wurzeln wäre  und das Produkt der Wurzeln
und das Produkt der Wurzeln 
2 Wir wissen, dass 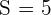 und
und 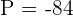 ist, daher ist
ist, daher ist
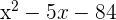
3 Löse die Gleichung zweiten Grades 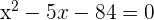
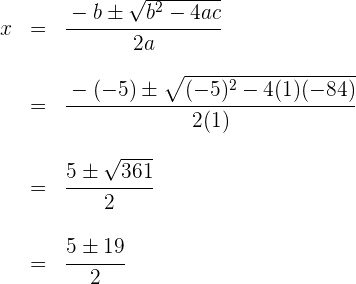
Die Wurzeln sind
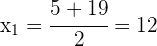
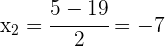
Die gesuchten Zahlen sind also  und
und 
In 11 Jahren wird Peter die Hälfte seines Alters vor 13 Jahren zum Quadrat haben.
Wie alt ist Peter?
1 Definiere die Variablen dieser Aufgabe:
Aktuelles Alter 
Alter vor 13 Jahren 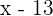
Alter in 11 Jahren 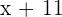
2 Stelle die zugehörige Gleichung auf:
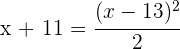
3 Bilde das Binom zum Quadrat, entferne die Nenner und du erhältst die Gleichung:
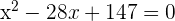
4 Löse die Gleichung
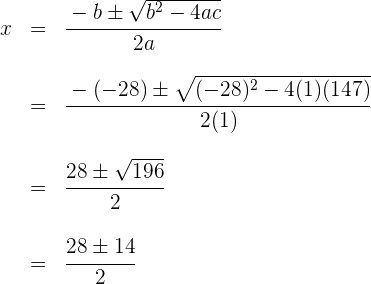
Die Wurzeln sind
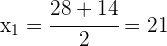

 ist keine mögliche Lösung, da das Alter dazu 13 Jahre vorher nicht existiert.
ist keine mögliche Lösung, da das Alter dazu 13 Jahre vorher nicht existiert.
Peters aktuelles Alter ist daher  Jahre.
Jahre.
Um ein rechteckiges Haus mit 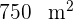 Fläche zu umzäunen, wurden
Fläche zu umzäunen, wurden  Zaun benötigt. Berechne die Maße des Hauses.
Zaun benötigt. Berechne die Maße des Hauses.
1 Stelle das Grundstück grafisch dar:

Halbperimeter 
Länge 
Höhe 
2 Die Fläche ist gleich die Länge mal Höhe:
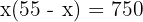
3 Löse die Klammer auf und bestimme die Wurzeln
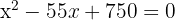
 und
und 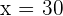
Die Maße des Hauses sind also:
Länge  und Höhe
und Höhe 
Länge  und Höhe
und Höhe 
Die drei Seiten eines Dreiecks sind proportional zu den Zahlen 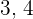 und
und  . Wie lang ist jede Seite, wenn die Fläche des Dreiecks
. Wie lang ist jede Seite, wenn die Fläche des Dreiecks 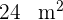 beträgt?
beträgt?
1 Stelle die Daten grafisch dar:
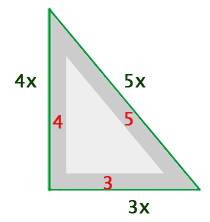
Seite 1  (Grundseite)
(Grundseite)
Seite 2  (Höhe)
(Höhe)
Seite 3 
2 Wende die Formel für die Dreiecksläche an:

3 Entferne die Nenner und löse die Gleichung

 ist keine Lösung, da die Länge der Seiten nicht negativ sein darf. Die Lösungen sind daher:
ist keine Lösung, da die Länge der Seiten nicht negativ sein darf. Die Lösungen sind daher:
Seite 1 
Seite 2 
Seite 3 
Ein rechteckiges Gartengelände mit  Länge mal
Länge mal 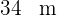 Breite ist gleichmäßig von einem Weg umgeben. Wie breit ist der Weg, wenn seine Fläche
Breite ist gleichmäßig von einem Weg umgeben. Wie breit ist der Weg, wenn seine Fläche 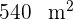 beträgt?
beträgt?
1 Stelle die Daten grafisch dar:

Die Breite des Weges definieren wir als 
2 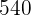 ist gleich die Gesamtfläche minus die Fläche des Gartens:
ist gleich die Gesamtfläche minus die Fläche des Gartens:
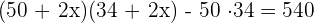
3 Löse die Klammer und vereinfache die Gleichung, indem du beide Seiten durch 4 teilst:
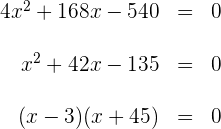
Der Weg ist also  breit.
breit.
 ist keine mögliche Lösung, da die Maße positiv sein müssen.
ist keine mögliche Lösung, da die Maße positiv sein müssen.
Berechne die Maße eines Rechtecks, dessen Diagonale  misst, und das ähnlich eines Rechtecks mit den Maßen
misst, und das ähnlich eines Rechtecks mit den Maßen 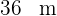 mal
mal  ist.
ist.
1 Die Seiten haben 12 als gemeinsamen Faktor, wodurch sich angesichts der Ähnlichkeit ergibt:
Länge 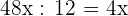
Breite 
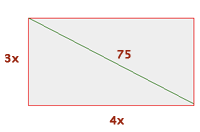
2 Wende den Satz des Pythagoras an:
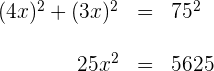
3 Löse die Gleichung auf und du erhältst 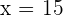 . Die Maße des gesuchten Rechtecks sind also:
. Die Maße des gesuchten Rechtecks sind also:
Länge 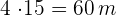
Breite 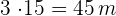
Finde die ganze Zahl, deren Summe mit ihrer Inversen gleich  ist.
ist.
1 Definiere:
gesuchte Zahl: 
Inverse der Zahl: 
2 Die Summe der Aufgabenstellung ist:
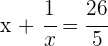
3 Löse die rationale Gleichung:
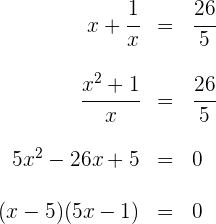
Die Lösungen der Gleichung sind  und
und 
Die gesuchte Zahl ist  , da
, da  keine ganze Zahl und somit keine mögliche Lösung ist.
keine ganze Zahl und somit keine mögliche Lösung ist.
Zwei natürliche Zaheln unterscheiden sich in zwei Einheiten. Die Summe ihrer Quadratzahlen ist 580. Welche Zahlen sind gesucht?
1 Definiere:
Zahl 1 
Zahl 2 
Die Summe ihrer Quadratzahlen ist:
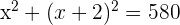
2 Berechne das Quadrat des Binoms, vereinfache die Gleichung, indem du beide Seiten durch 2 teilst:
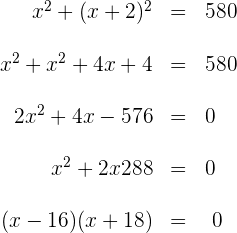
3 Die Lösungen der Gleichung sind  und
und 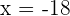
Zahl 1 
Zahl 2 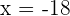
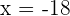 ist keine Lösung, da es sich nicht um eine natürliche Zahl handelt
ist keine Lösung, da es sich nicht um eine natürliche Zahl handelt
Ein Schwimmbecken kann über zwei Leitungen  und
und  innerhalb von 2 Stunden befüllt werden. Wenn man nur Leitung
innerhalb von 2 Stunden befüllt werden. Wenn man nur Leitung  verwendet, braucht man 3 Stunden weniger, als wenn man nur Leitung
verwendet, braucht man 3 Stunden weniger, als wenn man nur Leitung  verwendet. Wie lange benötigt man mit jeweils nur einer der beiden Leitungen?
verwendet. Wie lange benötigt man mit jeweils nur einer der beiden Leitungen?
1 Definiere:
Füllzeit mit 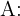

Füllzeit mit 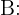

2 Innerhalb von einer Stunde passiert Folgendes:

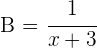
Es ist auch bekannt, dass man mit beiden Leitungen zusammen innerhalb von einer Stunde das halbe Schwimmbecken befüllen kann:

3 Setze ein:
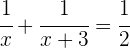
Wir erhalten eine rationale Gleichung. Um diese zu lösen, müssen zuerst die Nenner entfernt werden:
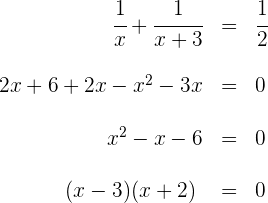
Die Lösungen sind  und
und  . Letztere kann aber keine Lösung sein, da die Zeit sonst negativ wäre.
. Letztere kann aber keine Lösung sein, da die Zeit sonst negativ wäre.
4 Prüfe, ob  eine mögliche Lösung ist:
eine mögliche Lösung ist:
Nach einer Stunde geschieht Folgendes:

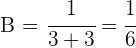
Nach zwei Stunden geschieht Folgendes
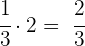

Somit wäre das Schwimmbecken innerhalb von 2 Stunden voll:
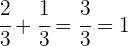
Die gesuchte Füllzeit ist daher:
Füllzeit von 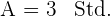
Füllzeit von 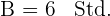
Die Seiten eines rechtwinkligen Dreiecks haben die Längen von drei konsekutiven Zahlen
Wie lang sind die Seiten?
1 Stelle die Daten grafisch dar:
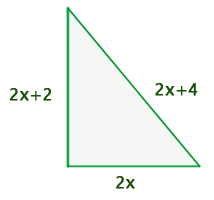
Erste Kathete 
Zweite Kathete 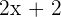
Hypotenuse 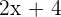
2 Wende den Satz des Pythagoras an:
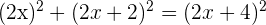
3 Bilde das Quadrat der Binome und vereinfache die Gleichung, indem du beide Seiten durch 4 teilst:
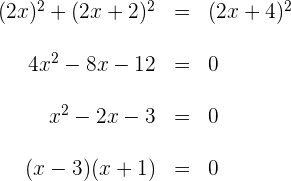
4 Die Lösungen der Gleichung sind 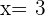 und
und 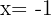 . Die Maße sind also
. Die Maße sind also 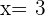
Erste Kathete 
Zweite Kathete 
Hypotenuse 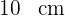
 wird nicht beachtet, da die Seitenlängen nicht negativ sein können.
wird nicht beachtet, da die Seitenlängen nicht negativ sein können.
Eine rechteckige Figur ist  länger als hoch. Mit ihr wird eine Kiste gebaut, deren Volumen
länger als hoch. Mit ihr wird eine Kiste gebaut, deren Volumen 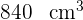 beträgt, indem ein Quadrat mit
beträgt, indem ein Quadrat mit  Seitenlänge an jeder Ecke abgeschnitten und die Seiten an den Kanten entlang gefaltet werden. Welches Volumen hat die Kiste?
Seitenlänge an jeder Ecke abgeschnitten und die Seiten an den Kanten entlang gefaltet werden. Welches Volumen hat die Kiste?
1 Stelle die Daten grafisch dar:
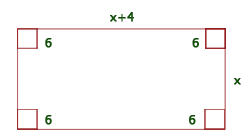
Breite: 
Länge: 
Höhe: 
2 Das Volumen der Kiste berechnet sich als: 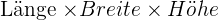
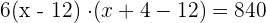 (x − 12) · (x −8) = 140
(x − 12) · (x −8) = 140
3 Löse die Gleichung:

Die Lösungen sind  und
und  . Die gesuchten Maße sind daher:
. Die gesuchten Maße sind daher:
Breite: 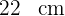
Länge: 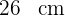
Die Lösung  ist nicht gültig, da die Maße nicht negativ sein können.
ist nicht gültig, da die Maße nicht negativ sein können.
Ein Behälter wir mit zwei Leitungen innerhalb von 1 Stunde und 20 Minuten komplett gefüllt. Einzeln benötigt man mit einer Leitung zwei Stunden länger als mit der anderen. Wie lange benötigt man, um mit nur einer der Leitungen den Behälter zu füllen?
1 Definiere:
Füllzeit Leitung 1: 
Füllzeit Leitung 2: 
2 Innerhalb von einer Stunde passiert Folgendes:
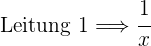
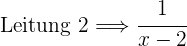
Wir wissen außerdem, dass man den Behälter innerhalb von 1 Stunde und 20 Minuetn mit beiden Leitungen füllen kann, d.h. in  Stunden
Stunden
3 Setze ein:
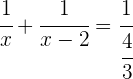
Wir erhalten eine rationale Gleichung. Um diese zu lösen, müssen zuerst die Nenner entfernt werden:
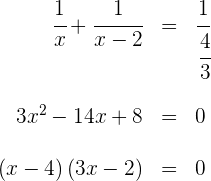
Die Lösungen sind  und
und  . Letztere ist keine mögliche Lösung, da die Füllzeit der zweiten Leitung dann negativ wäre.
. Letztere ist keine mögliche Lösung, da die Füllzeit der zweiten Leitung dann negativ wäre.
4 Die gesuchten Zeiten sind also:
Füllzeit Leitung 1: 
Füllzeit Leitung 2: 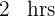
Mit KI zusammenfassen:



