Definition der Gleichung 1. Grades (lineare Gleichung)
Eine Gleichung 1. Grades (auch als lineare Gleichung bezeichnet, da der Graph der Gleichung eine Gerade ergibt) ist eine Gleichheit zweier algebraischer Ausdrücke mit einer oder mehreren Unbekannten (alle mit dem Exponenten 
), deren Werte durch arithmetische Operationen in Beziehung gesetzt werden können.
Aufgaben zu linearen Gleichungen
1 
Wir bestimmen die Unbekannte, indem wir beide Glieder durch 
dividieren. Praktisch gesehen kann man auch sagen, dass die , die im ersten Glied multipliziert, im zweiten Glied dividiert.
2 
Wenn wir gleichartige Terme zusammenfassen, müssen wir die beiden Glieder mit 
und 
addieren, um eine äquivalente Gleichung zu erhalten.
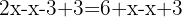
In der Praxis heißt das: Um einen Term auf die andere Seite zu bringen, müssen wir auf beiden Seiten der Gleichung dieselben Rechenschritte durchführen. Wir erhalten also:
3 
Um die Klammer aufzulösen, wenden wir das Distributivgesetz an. Wir multiplizieren also jeden algebraischen Term der Klammer mit und erhalten auf der linken Seite der Gleichung: 
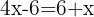
Wir fassen gleichartige Terme zusammen. Das x bringen wir durch Subtraktion auf die linke Seite und die 
durch Addition auf die rechte Seite der Gleichung:
Wir bestimmen die Unbekannte. Die , mit der auf der linken Seite multipliziert wird, bringen wir durch Division auf die rechte Seite
4 
Damit wir die Nenner beseitigen können, müssen wir das kleinste gemeinsame Vielfache von und bestimmen
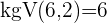
Wir multiplizieren beide Glieder der Gleichung mit dem kgV, in diesem Fall , und erhalten:
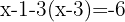
Wir wenden das Distributivgesetz an, um die Klammer aufzulösen. Wir fassen gleichartige Terme zusammen und addieren:
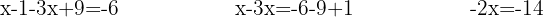
Wir bestimmen die Unbekannte:
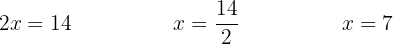
5 
Wir multiplizieren 
mit jedem Term der Klammer (Distributivgesetz), um die Klammer aufzulösen und vereinfachen:
Wir fassen gleichartige Terme zusammen und addieren:
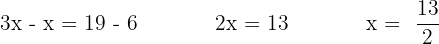
6 
Wir wenden das Distributivgesetz an, um die Klammern aufzulösen. Hierzu multiplizieren wir die erste Klammer mit 
und die zweite Klammer mit 
.
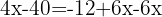
Wir fassen gleichartige Terme zusammen
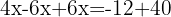
Wir addieren die gleichartigen Terme und bestimmen
7 
Wir wenden das Distributivgesetz an, um die Klammern aufzulösen. Hierzu multiplizieren wir die erste Klammer mit und die zweite Klammer mit 
.
Wir fassen gleichartige Terme zusammen
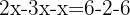
Wir addieren die gleichartigen Terme und bestimmen
8 
Um die Nenner beseitigen zu können, müssen wir das kleinste gemeinsame Vielfache von , 
und 
bestimmen
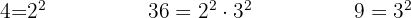
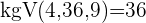
Wir dividieren den gemeinsamen Nenner durch jeden Nenner und multiplizieren das Ergebnis mit dem entsprechenden Zähler
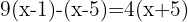
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Wir multiplitzieren die erste Klammer mit , die zweite mit 
und die dritte mit.
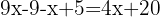
Wir fassen gleichartige Terme zusammen
Wir addieren die gleichartigen Terme und bestimmen
9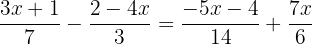 
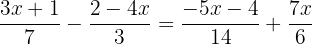
Um die Nenner beseitigen zu können, müssen wir das kleinste gemeinsame Vielfache von 
,,
und bestimmen.
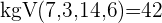
Wir dividieren den gemeinsamen Nenner durch jeden Nenner und multiplizieren das Ergebnis mit dem entsprechenden Zähler
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit , die zweite mit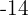 
und die dritte mit .
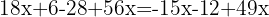
Wir fassen gleichartige Terme zusammen
Wir addieren die gleichartigen Terme und bestimmen
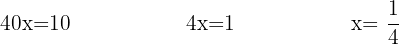
10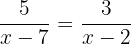 
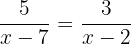
Damit die Gleichheit der beiden Brüche erfüllt ist, muss das Produkt der Zähler gleich dem Produkt der Nenner sein.
Alternativ können wir auch das kgV bestimmen, das hier 
ist, da die beiden Binome irreduzibel sind. Danach dividieren wird das kgV durch jeden Nenner und das Ergebnis multiplizieren wir mit dem entsprechenden Zähler.
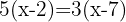
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit 
und die zweite mit .
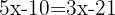
Wir addieren die gleichartigen Terme
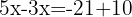
Wir bestimmen die Unbekannte:
11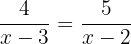 
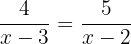
Damit die Gleichheit der beiden Brüche erfüllt ist, muss das Produkt der Zähler gleich dem Produkt der Nenner sein.
Alternativ können wir auch das kgV bestimmen, das hier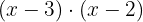 
ist, da die beiden Binome irreduzibel sind. Danach dividieren wird das kgV durch jeden Nenner und das Ergebnis multiplizieren wir mit dem entsprechenden Zähler.
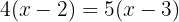
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit und die zweite mit .
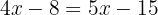
Wir fassen gleichartige Terme zusammen
Wir bestimmen die Unbekannte:
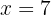
12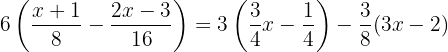 
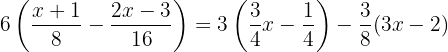
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit , die zweite mit und die dritte mit 
.
Wir dürfen nicht vergessen, dass die Multiplikation einer ganzen Zahl mit einem Bruch durch die Multiplikation mit der ganzen Zahl mit dem Zähler des Bruch gelöst wird und der Nenner gleich bleibt.
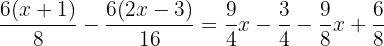
Wir wenden das Distributivgesetz an, um die Klammern in den Zählern aufzulösen
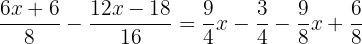
Um die Nenner zu beseitigen, bestimmen wir das kleinste gemeinsame Vielfache von , 
und 
.
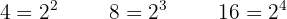
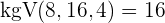
Wir dividieren den gemeinsamen Nenner durch jeden Nenner und multiplizieren das Ergebnis mit dem entsprechenden Zähler.
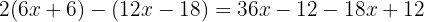
Um die Klammer aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit und vereinfachen (hierbei achten wir auf den Vorzeichenwechsel).
Wir fassen gleichartige Terme zusammen
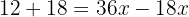
Wir bestimmen die Unbekannte:
13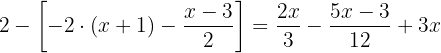 
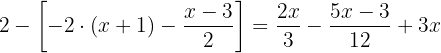
In diesem Fall ist es sinnvoll, wenn wir uns zuerst um den Ausdruck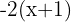 
kümmern. So können wir die eckige Klammer auflösen und erhalten eine runde Klammer.
Wir multiplizieren die Terme in der Klammer mit −1, um das negative Vorzeichen loszuwerden und die Klammer aufzulösen:
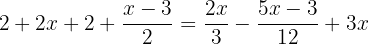
Um die Nenner zu beseitigen, müssen wir das kleinste gemeinsame Vielfache von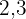 
und 
bestimmen.
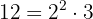
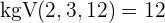
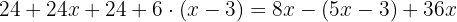
Um die Klammern aufzulösen, wenden wir das Distributivgesetz an. Hierzu multiplizieren wir die erste Klammer mit und die zweite mit :
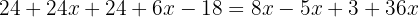
Wir fassen gleichartige Terme zusammen:
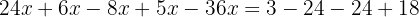
Wir addieren:
Wir dividieren beide Glieder durch: 
14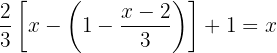 
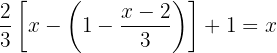
Wir multiplizieren die Terme in der Klammer mit , um das negative Vorzeichen loszuwerden und die Klammer aufzulösen. Nun haben wir aus der eckigen Klammer eine runde Klammer gemacht.
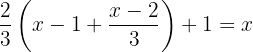
Um die Klammer aufzulösen, wenden wir das Distributivgesetz an.
Wir müssen beachten, dass wenn wir einen Bruch mit einem anderen Bruch multiplizieren, der Zähler mit dem Zähler und der Nenner mit dem Nenner multipliziert werden muss.
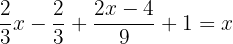
Um die Nenner zu beseitigen, müssen wir das kleinste gemeinsame Vielfach von und bestimmen.
Wir fassen gleichartige Terme zusammen:
Wir addieren und bestimmen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
