Zur Erinnerung: Biquadratische Gleichungen haben folgende Form:
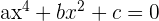
mit .
Diese Gleichungen werden mit Hilfe der Variablenänderung , gelöst, der die Gleichung in eine quadratische Gleichung umgewandelt.
Biquadratische Gleichungen
1
Nimm zuerst die Variablenänderung vor.
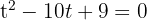
Löse nun die erhaltene quadratische Gleichung mit Hilfe der allgemeinen Formel.
Das heißt:
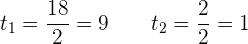
Mache dann die Variablenänderung rückgängig, um die Lösungen der biquadratischen Gleichung zu finden:
Daher hat diese biquadratische Gleichung die folgenden vier reellen Lösungen:
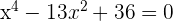
Du hast die folgende Gleichung:
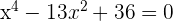
Nimm zuerst die Variablenänderung vor:
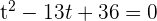
Löse die erhaltene quadratische Gleichung:
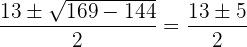
Das heißt:
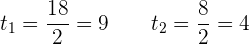
Mache nun due die Variablenänderung rückgängig, um die Lösungen der biquadratischen Gleichung zu finden:
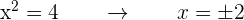
Die biquadratische Gleichung hat also vier reelle Lösungen:
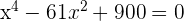
In diesem Fall lautet die Gleichung:
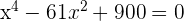
Nimm zunächst die Variablenänderung vor:
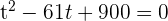
Löse dann die erhaltene quadratische Gleichung:
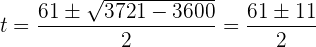
Also so:
Mache auch hier die Variablenänderung rückgängig:
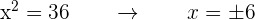
Somit hat diese biquadratische Gleichung die folgenden vier reellen Lösungen
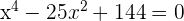
In diesem Fall lautet die Gleichung:
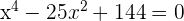
Ändere die Variable:
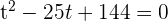
Löse die erhaltene quadratische Gleichung:
Somit
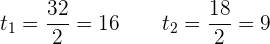
Mache die Variablenänderung rückgängig:
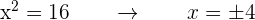
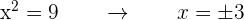
Diese biquadratische Gleichung hat vier reelle Lösungen:
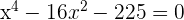
Die Gleichung lautet:
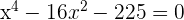
Ändere auch hier die Variable:
Löse die erhaltene quadratische Gleichung:
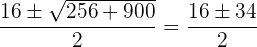
Deshalb:
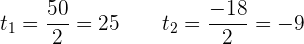
Mache die Variablenänderung rückgängig:
In diesem Fall hat die biquadratische Gleichung nur zwei reelle Lösungen:
Wie biquadratische Gleichungen wird eine Gleichung der Form
mit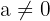 
als triquadratische Gleichung bezeichnet. Diese Art von Gleichung wird mit Hilfe der Variablenänderung 
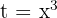gelöst.
6
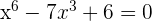
Die Gleichung lautet:
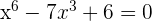
Ändere die Variable:
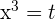
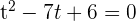
Löse die erhaltene quadratische Gleichung:
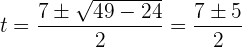
Das heißt:
Mache die Variablenänderung rückgängig, um die Lösungen der Gleichung zu finden:
![x^3 = 6 \qquad \to \qquad x_1 = \sqrt[3]{6}, \quad x_2, x_3 \notin \mathbb{R}](https://www.superprof.de/lernplattform/wp-content/ql-cache/quicklatex.com-96c8df350e12883f34dbce99f14218f3_l3.png "Rendered by QuickLaTeX.com")
![x^3 = 1 \qquad \to \qquad x_4 = \sqrt[3]{1} = 1, \quad x_5, x_6 \notin \mathbb{R}](https://www.superprof.de/lernplattform/wp-content/ql-cache/quicklatex.com-eff9c318cd61dafb938d1a4eeeca1984_l3.png "Rendered by QuickLaTeX.com")
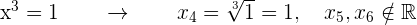
In diesem Fall hat die triquadratische Gleichung nur zwei reelle Lösungen:
![x_1 = \sqrt[3]{6}, \quad x_4 = 1, \quad x_2, x_3, x_5, x_6 \notin \mathbb{R}](https://www.superprof.de/lernplattform/wp-content/ql-cache/quicklatex.com-43f5b5e35ac9faab84fd799189235cea_l3.png "Rendered by QuickLaTeX.com")
Die Plattform, die Lehrer/innen und Schüler/innen miteinander verbindet
Du findest diesen Artikel toll? Vergib eine Note!
Loading...