1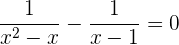
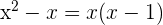
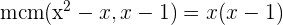
1 Berechne das kleinste gemeinsame Vielfache der NennerBringe es auf einen gemeinsamen Nenner. Berechne dazu das kleinste gemeinsame Vielfache der Nenner

2 Gleichung ohne rationale Zahlen darstellen

Dividiere das kleinste gemeinsame Vielfache zwischen jedem Nenner und multipliziere das Ergebnis mit dem entsprechenden Zähler. Aus diesem Verfahren erhälst Du folgende Gleichung:

3 Prüfen der Lösung

Setze die erhaltene Lösung ein, um zu überprüfen, dass die Gleichung erfüllt ist

Die Gleichung hat keine Lösung, da sich für x = 1 die Nenner aufheben.

2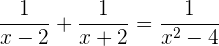
1 Berechne das kleinste gemeinsame Vielfache der Nenner

Bringe es auf einen gemeinsamen Nenner. Berechne dazu das kleinste gemeinsame Vielfache der Nenner

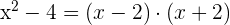
2 Gleichung ohne rationale Zahlen darstellen

Dividiere das kleinste gemeinsame Vielfache durch jeden Nenner und multipliziere das Ergebnis dann mit dem entsprechenden Zähler

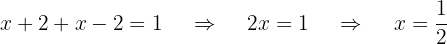
3 Prüfen der Lösung

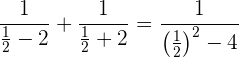
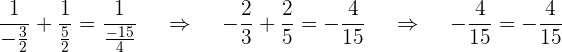
Die Lösung ist: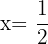

3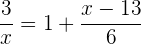
1 Berechne das kleinste gemeinsame Vielfache der Nenner

Bringe es auf einen gemeinsamen Nenner. Berechne dazu das kleinste gemeinsame Vielfache der Nenner

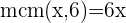
2 Gleichung ohne rationale Zahlen darstellen

Teile das kleinste gemeinsame Vielfache durch jeden Nenner und multipliziert dann das Ergebnis mit dem entsprechenden Zähler

Greife für die Lösungen auf die abc-Formel für quadratische Gleichungen zurück

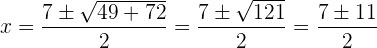
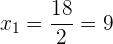
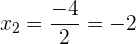
3 Prüfen der Lösung

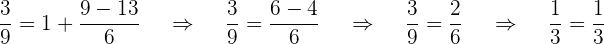
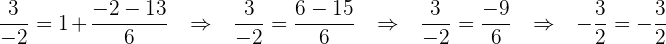
4 Gesucht wird eine ganze Zahl, deren Summe ihrem Kehrwert gleich ist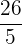
1 Stelle die Gleichung auf

steht für die gesuchte Zahl

Kehrwert der Zahl:

Summe aus einer Zahl und ihrem Kehrwert:

2 Nenner entfernen

Da es sich um eine rationale Gleichung, musst du zunächst die Nenner entfernen

3 Gleichung lösen

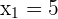
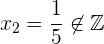
4 Ergebnis überprüfen

Die gesuchte Zahl ist 5, aber da es sich um eine rationale Gleichung handelt, musst Du dies überprüfen:

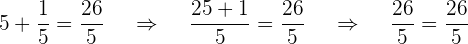
ist keine Lösung, da es sich nicht um eine ganze Zahl handelt

5 Zwei Rohre A und B füllen gemeinsam ein Schwimmbecken in zwei Stunden. A benötigt dafür drei Stunden weniger als B. Wie viele Stunden benötigt jedes einzelne Rohr dafür??
1 Gleichung aufstellen

Zeit, die A benötigt

Zeit, die B benötigt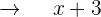

Zeit, die A und B zusammen benötigen

Geschwindigkeit, mit der A auffüllt \hspace{.5cm}\rightarrow \hspace{.5cm} \frac{1}{x}[/latex]

Geschwindigkeit, mit der B auffüllt 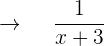Geschwindigkeit, mit der A und B auffüllen 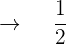Da Rohr A und Rohr B das Becken zusammen in zwei Stunden füllen, wird die Füllgeschwindigkeit der beiden addiert und man erhält:

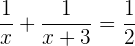
2 Nenner entfernen

Da es sich um eine rationale Gleichung handelt, musst du die Nenner entfernen

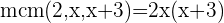
3 Gleichung lösen

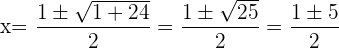
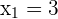
4 Ergebnis überprüfen

Prüfe, ob 3 eine Lösung ist:

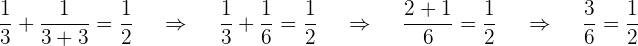
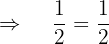
Zeit von A 3 Stunden

Zeit von B 6 Stunden

6 Ein Rohr braucht zwei Stunden länger als das andere, um einen Tank zu füllen, und wenn beide zusammen auffüllen benötigen sie 1 Stunde und 20 Minuten. Wie lange wird es dauern, bis jedes einzelne Rohr den Tank aufgefüllt hat?
1 Gleichung aufstellen

Verschiebe die Zeit auf einen Bruchteil einer Stunde

1 Stunde und 20 Minuten = 4/3 Stunden

Zeit des 1. Rohres: x

Zeit des 2. Rohres: x − 2

Zeit für beide Rohre:

Geschwindigkeit von Rohr 1:

Geschwindigkeit von Rohr 2:

Geschwindigkeit beider Rohre zusammen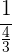

Da die Rohre zusammen das Becken in Std. füllen, wird die Füllgeschwindigkeit jedes einzelnen Rohres addiert und man erhält::

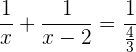
Auf der anderen Seite der Gleichung kehrt man den Bruch um

2 Nenner entfernen

Man entfernt den Nenner, das kleinste gemeinsame Vielfache ist: 4x(x − 2)

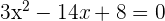
3 Gleichung lösen

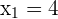
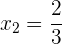
Benötigte Zeit des ersten Rohres: 4 Stunden

Zeit des zweiten Rohres 2 Stunden

Es stellt sich heraus, dass keine Lösung ist, da die Zeit, die das zweite Rohr benötigt, negativ wäre.

Mit KI zusammenfassen:

Du findest diesen Artikel toll? Vergib eine Note!

4,00 (10 Note(n))
Loading...

Chantal

Sprachen, Literatur, Theater und Musik sind meine große Leidenschaft und waren schon immer ein wichtiger Teil meines schulischen, beruflichen und privaten Werdeganges.