Aufgaben mit Lösungen
Eine Uhr schlägt 3 Uhr. Zu welchem Zeitpunkt zwischen 3 und 4 Uhr überschneiden sich die Zeiger?
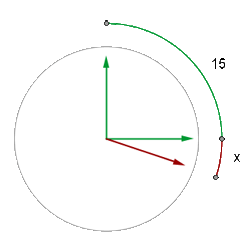
x ist der durch den Stundenzeiger beschriebene Bogen.
(15 + x) x ist der durch den Minutenzeiger beschriebene Bogen.
Der Winkel oder Bogen, den der Minutenzeiger beschreibt, ist immer 12 Mal größer als der Bogen, den der Stundenzeiger beschreibt
15 + x = 12x
x = 15/11 min = 1,36 min − 1min = 0,36
Wir multiplizieren die 0,36 Minuten mit 60 Sekunden und erhalten 21 Sekunden
Die Zeige überschneiden sich 1 Minute und 21 Sekunden nach Viertel nach 3: 3 h 16 min 21 s
Eine Uhr schlägt 2 Uhr. Zu welchem Zeitpunkt bilden die Zeiger zum ersten Mal einen rechten Winkel?
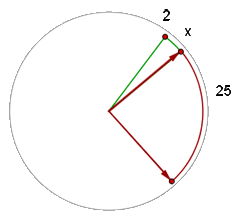
Die Zeiger der Uhr bilden einen rechten Winkel bei 2 h 25 min und ein wenig mehr, das wir x nennen.
x ist der durch den Stundenzeiger beschriebene Bogen.
25 + x ist der durch den Minutenzeiger beschriebene Bogen.
Der Winkel oder Bogen, den der Minutenzeiger beschreibt, ist immer 12 Mal größer als der Bogen, den der Stundenzeiger beschreibt.
25 + x = 12x
x = 25/11 min = 2,27 min − 2 min = 0,27
Wir multiplizieren die 0,27 Minuten mit 60 und erhalten 16 Sekunden
Die Zeiger überschneiden sich 2 Minuten und 21 Sekunden nach 2 h 25 min: 2h 27 min 16 s
Zwei Städte A und B sind 300 km voneinander entfernt. Um 9 Uhr morgens fährt ein Auto mit einer Geschwindigkeit von 90 km/h von Stadt A nach Stadt B, und von Stadt B fährt ein anderes Auto mit einer Geschwindigkeit von 60 km/h nach Stadt A. Berechne:
a Die Zeit, die benötigt wird, bis sie aufeinandertreffen.
Die Strecke ist gleich der Geschwindigkeit mal der Zeit, d. h. die Strecke, die der eine zurücklegt, beträgt 90t und die Strecke, die der andere zurücklegt, 60t.
Wir wissen, dass die Strecke, die das erste Auto zurücklegt, plus die Strecke, die das zweite Auto zurücklegt, 300 km beträgt
90t + 60t = 300 150t = 300 t = 2 Stunden
b Die Uhrzeit des Aufeinandertreffens.
Sie treffen um 11 Uhr aufeinander, da sie um 9 Uhr morgens losfahren und es zwei Stunden dauert, bis sie aufeinandertreffen.
c Die von jedem zurückgelegte Strecke.
e AB = 90 · 2 = 180 km
e BC = 60 · 2 = 120 km
Zwei Städte A und B sind 180 km voneinander entfernt. Um 9 Uhr morgens fährt in jeder Stadt ein Auto ab, und die beiden Autos fahren in dieselbe Richtung. Das Auto, das aus A kommt, fährt mit 90 km/h, das aus B mit 60 km/h. Berechne:
a Die Zeit, die benötigt wird, bis sie aufeinandertreffen.
Die Strecke ist gleich der Geschwindigkeit mal der Zeit, d. h. die Strecke, die der eine zurücklegt, beträgt 90t und die Strecke, die der andere zurücklegt, 60t.
Die vom ersten Auto zurückgelegte Strecke minus die vom zweiten Auto zurückgelegte Strecke beträgt 180 km.
90t − 60t = 180 30t = 180 t = 6 Stunden
b Die Uhrzeit des Aufeinandertreffens.
Sie treffen um 15 Uhr aufeinadner, da sie um 9 Uhr losfahren und nach 6 Stunden Fahrt aufeinandertreffen.
c Die von jedem zurückgelegte Strecke.
eAB = 90 · 6 = 540 km
eBC = 60 · 6 = 360 km
Ein Auto verlässt die Stadt A mit einer Geschwindigkeit von 90 km/h. Drei Stunden später verlässt ein anderes Auto dieselbe Stadt und verfolgt das erste Auto mit einer Geschwindigkeit von 120 km/h. Berechne:
a Die Zeit, die benötigt wird, bis sie aufeinandertreffen.
Wenn die Zeit, die das erste Auto benötigt, t ist, ist die Zeit, die das zweite Auto benötigt, das drei Stunden später abfährt, t - 3
Die Strecke ist gleich der Geschwindigkeit mal der Zeit, d. h. die von der ersten Person zurückgelegte Strecke ist 90t und die von der zweiten Person zurückgelegte Strecke ist 120(t - 3).
90t = 120 · (t − 3)
90t = 120t − 360 −30t = −360 t = 12 Stunden
Das erste Auto benötigt 12 h.
Das zweite Auto benötigt (12 − 3) = 9 h.
b Die zurückgelegte Strecke zum Zeitpunkt des Aufeinandertreffens.
Wir berechnen die von einem der beiden zurückgelegte Strecke
e1 = 90 · 12 = 1080 km
Ein LKW verlässt eine Stadt mit einer Geschwindigkeit von 40 km/h. Eine Stunde später verlässt ein Auto dieselbe Stadt in dieselbe Richtung und mit 60 km/h. Berechne:
a Die Zeit, die benötigt wird, bis sie aufeinandertreffen.
e1 = e2
Wenn die Zeit, die der erste LKW benötigt, t ist, dann ist die Zeit, die der zweite LKW, der eine Stunde später abfährt, benötigt, t − 1.
Die Strecke ist gleich der Geschwindigkeit mal der Zeit, d. h. die von der ersten Person zurückgelegte Strecke ist 40t und die von der zweiten Person zurückgelegte Strecke ist 60(t - 1).
40t = 60 (t − 1)
40t = 60t − 60 40t − 60t = −60 −20t = −60
t = 3h
Da das Auto eine Stunde später abfährt, dauert es 2 Stunden, bis es den LKW erreicht.
b Zurückgelegte Strecke bis zum Aufeinandertreffen.
Wir berechnen die von einem der beiden zurückgelegte Strecke
e1 = 40 · 3 = 120 km .
Zwei Radfahrer fahren morgens um 9 Uhr von den Orten A und B, die 130 km voneinander entfernt sind, in entgegengesetzter Richtung los. Der Radfahrer, der A verlässt, fährt mit einer konstanten Geschwindigkeit von 30 km/h, der Radfahrer, der B verlässt, fährt mit 20 km/h. Wie weit von A entfernt werden sie sich treffen und zu welcher Zeit?
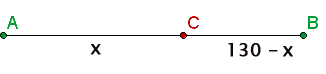
Die Strecke ist gleich der Geschwindigkeit mal der Zeit, d. h. der von der ersten Person zurückgelegte Weg beträgt 30t und der von der zweiten Person zurückgelegte Weg 20t.
Wir wissen, dass der von der ersten Person zurückgelegte Weg plus der von der zweiten Person zurückgelegte Weg 130 km beträgt
30t + 20t = 130 50t = 130
t = 130/50 = 2 h 36 min
Sie treffen um 11:36 Uhr aufeinander, weil sie um 9.00 Uhr losfahren und es 2 Stunden und 36 Minuten dauert, bis sie sich treffen.
e AC = 30 · 130/50 = 78 km
Ein Wasserhahn braucht drei Stunden, um einen Tank zu füllen, ein anderer vier Stunden. Wie lange brauchen die beiden Wasserhähne zusammen, um den Tank zu füllen?
In einer Stunde füllt der erste Hahn 1/3 des Tanks.
In einer Stunde füllt der zweite Hahn 1/4 des Tanks.
In einer Stunde füllen beide Hähne zusammen:
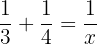
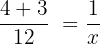
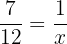
7x = 12 x = 12/7 Stunden
Ein Händler hat zwei Kaffeesorten im Angebot, von denen die erste 40 € pro kg und die zweite 60 € pro kg kostet. Wie viele Kilogramm von jeder Kaffeesorte muss man nehmen, um 60 Kilogramm der Mischung zu 50 € pro kg zu erhalten?
| 1. Klasse | 2. Klasse | gesamt | |
|---|---|---|---|
| Anzahl kg | x | 60 − x | 60 |
| Wert | 40 · x | 60 · (60 − x) | 60 · 50 |
Das Gewicht des ersten Kaffees mal seinem Preis plus das Gewicht des zweiten Kaffees mal seinem Preis ergibt das Gesamtgewicht des Kaffees multipliziert mit dem Preis der Mischung
40x + 60 · (60 − x) = 60 · 50
40x + 3600 − 60x = 3000; − 60x + 40x = 3000 − 3600; 20x = 600
x = 30; 60 − 30 = 30
Es müssen 30 kg der 1. Klasse und 30 kg der 2. Klasse gemischt werden.
Man hat zwei Silberbarren, einen der Güteklasse 0,750 und einen der Güteklasse 0,950. Welches Gewicht muss man von jedem Barren nehmen, um 1800 g Silber der Güteklasse 0,900 zu erhalten?
| 1. Klasse | 2. Klasse | gesamt | |
|---|---|---|---|
| Anzahl kg | x | 1800 − x | 1800 |
| Silber | 0,750 · x | 0,950 · (1800−x) | 0,900 · 1800 |
0,750 · x + 0,950 · (1800 − x) = 0,9 · 1800
0,750x + 1710 − 0,950x = 1 620
0,750x − 0,950x = 1620 − 1710
−0,2x = − 90 x = 450
1. Klasse 450 g
2. Klasse 1350 g
Ein Goldbarren der Güteklasse 0,950 wiegt 6 300 g. Wie viel reines Kupfer muss hinzugefügt werden, um seine Güteklasse auf 0,900 zu senken?
| Gold | Kupfer | gesamt | |
|---|---|---|---|
| Anzahl g | 6 300 | x | 6 300 + x |
| pures Gold | 0,950 · 6 300 | 0,900 · (6 300 + x) |
0,900 · (6 300 + x) = 0,950 · 6 300
5 670 + 0,900x = 5 985
0,900x = 315 x = 315/0,900 = 350
Kupfer 350 g
Mit KI zusammenfassen:


