Kapitel
Eine Gleichung 2. Grades hat immer folgende Form:
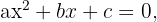 mit
mit 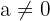

Lösen von Gleichungen 2. Grades
Die Gleichung 2. Grades wird mit der folgenden Formel gelöst:
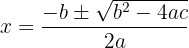
Beispiel: Bestimme die Lösungen für 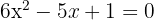
1 Zunächst ermitteln wir die Werte der Koeffizienten
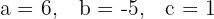
2 Wir setzen die Werte in die Formel ein und lösen

3 Wir stellen fest, dass wir für  zwei Lösungen erhalten. Diese werden gewöhnlich mit
zwei Lösungen erhalten. Diese werden gewöhnlich mit  ausgedrückt
ausgedrückt
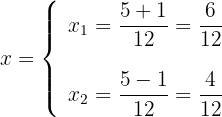
4 Wir vereinfachen die Ergebnisse und erhalten
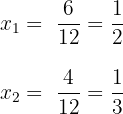
Diskriminante und Arten von Lösungen
Der Radikand der Quadratwurzel kommt in der Formel zur Lösung von quadratischen Gleichungen vor und wird als Diskriminante bezeichnet.
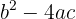
Anhand der Diskriminante lässt sich die Art der Lösungen der Gleichung 2. Grades bestimmen.
1 Wenn 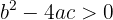 , sind
, sind 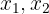 unterschiedliche reelle Lösungen.
unterschiedliche reelle Lösungen.
2 Wenn 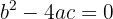 , hat die Gleichung genau eine Lösung.
, hat die Gleichung genau eine Lösung.
3 Wenn 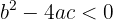 , hat die Gleichung keine reelle Lösung.
, hat die Gleichung keine reelle Lösung.
Beispiel: Bestimme die Arten der Lösungen für 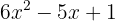
Die Koeffizienten sind 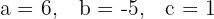
Wir setzen die Werte in die Formel ein und lösen
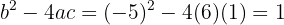
Da die Diskriminante größer als null ist, hat die Gleichung zweiten Grades zwei unterschiedliche reelle Lösungen.
Aufgaben zu Gleichungen 2. Grades anhand ihrer Lösungen
Bestimme die Gleichungen 2. Grades, die folgende Lösungen haben:

1 Wenn uns die Nullstellen  der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
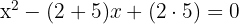
3 Die gesuchte Gleichung lautet somit
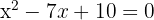

1 Wenn uns die Nullstellen  der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten

3 Die gesuchte Gleichung lautet somit

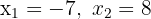
1 Wenn uns die Nullstellen 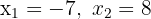 der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten

3 Die gesuchte Gleichung lautet somit

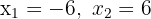
1 Wenn uns die Nullstellen 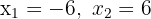 der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
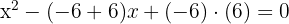
3 Die gesuchte Gleichung lautet somit


1 Wenn uns die Nullstellen  der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
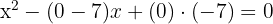
3 Die gesuchte Gleichung lautet somit

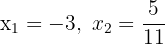
1 Wenn uns die Nullstellen 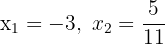 der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
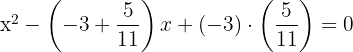
3 Die gesuchte Gleichung lautet somit

4 Die vorhergehende Gleichung kann mit ganzzahligen Koeffizienten ausgedrückt werden, indem beide Seiten der Gleichung mit  multipliziert werden
multipliziert werden

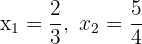
1 Wenn uns die Nullstellen 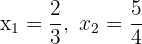 der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
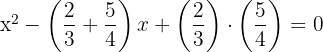
3 Die gesuchte Gleichung lautet somit

4 Die vorhergehende Gleichung kann mit ganzzahligen Koeffizienten ausgedrückt werden, indem man beide Seiten der Gleichung mit  multipliziert
multipliziert
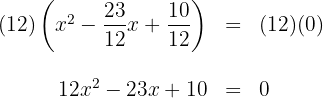
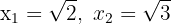
1 Wenn uns die Nullstellen 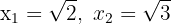 der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken
der Gleichung 2. Grades bekannt sind, können wir diese wie folgt ausdrücken

2 Wir setzen die Nullstellen ein und erhalten
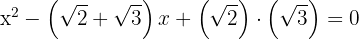
3 Die gesuchte Gleichung lautet somit
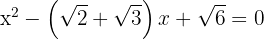
Aufgaben zur Faktorisierung von Gleichungen 2. Grades
Faktorisiere die folgenden Gleichungen 2. Grades
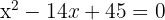
1 Die Koeffizienten sind:  .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen
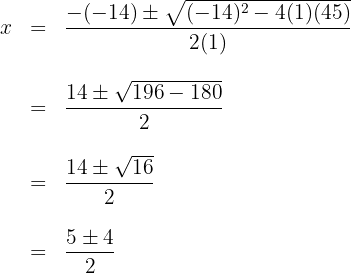
3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
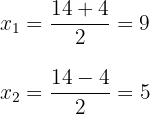
4 Die gesuchte Faktorisierung ist gegeben durch: 
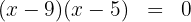
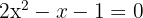
1 Die Koeffizienten sind: 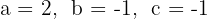 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen
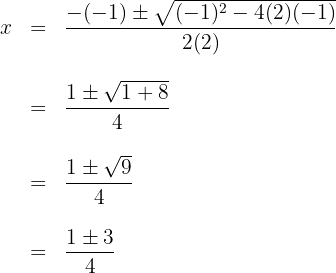
3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
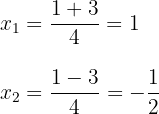
4 Die gesuchte Faktorisierung ist gegeben durch: 
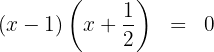
5 Wir können die Faktoren mit ganzzahligen Koeffizienten erhalten, indem wir den zweiten Faktor mit einem gemeinsamen Nenner schreiben und dann beide Seiten der Gleichung mit diesem Nenner multiplizieren.
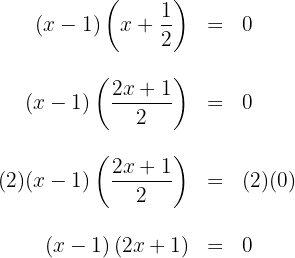
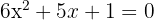
1 Die Koeffizienten sind: 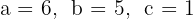 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen
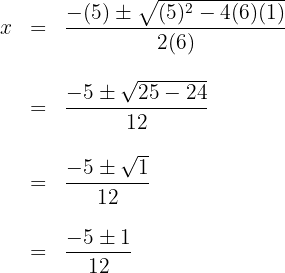
3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
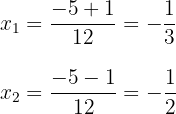
4 Die gesuchte Faktorisierung ist gegeben durch: 

5 Wir können die Faktoren mit ganzzahligen Koeffizienten erhalten, indem wir jeden Faktor mit einem gemeinsamen Nenner schreiben und dann beide Seiten der Gleichung mit dem Produkt der beiden Nenner multiplizieren.
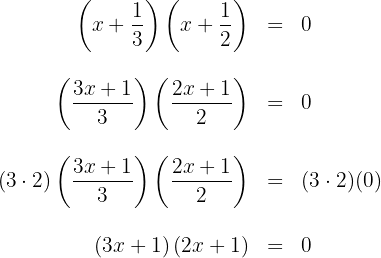

1 Die Koeffizienten sind: 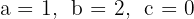 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen

3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
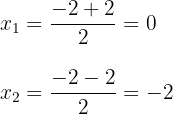
4 Die gesuchte Faktorisierung ist gegeben durch: 
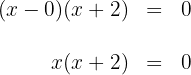
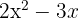
1 Die Koeffizienten sind: 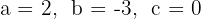 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen

3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden

4 Die gesuchte Faktorisierung ist gegeben durch: 
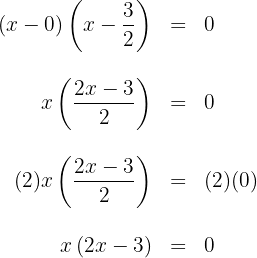
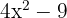
1 Die Koeffizienten sind: 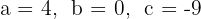 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen
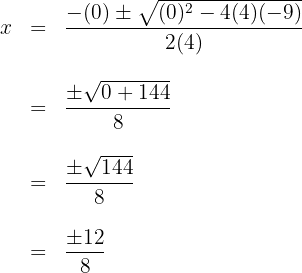
3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
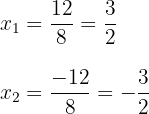
4 Die gesuchte Faktorisierung ist gegeben durch: 
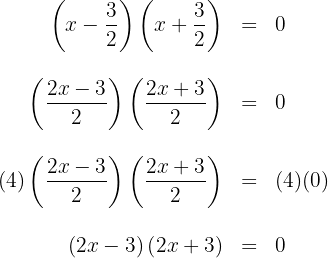
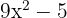
1 Die Koeffizienten sind: 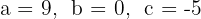 .
.
2 Wir setzen die Werte in die Formel ein, um die Lösungen zu erhalten und lösen
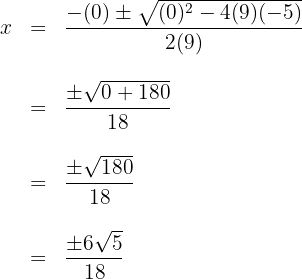
3 Wir erhalten zwei Werte für  , die mit
, die mit  ausgedrückt werden
ausgedrückt werden
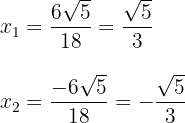
4 Die gesuchte Faktorisierung ist gegeben durch: 

Mit KI zusammenfassen:













