Das Gauß-Verfahren besteht darin, die Reduktionsmethode so anzuwenden, dass du in jeder Gleichung eine Unbekannte weniger hast als in der vorhergehenden Gleichung. Nimm das folgende Gleichungssystem und löse es schrittweise mit der Gaußschen Methode:
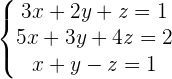
1 Setze als erste Gleichung diejenige mit dem Koeffizienten von  ein:
ein:  oder
oder  , wenn dies nicht möglich ist, machst du es mit
, wenn dies nicht möglich ist, machst du es mit  oder
oder  , wobei sich die Reihenfolge der Unbekannten ändert.
, wobei sich die Reihenfolge der Unbekannten ändert.

2 Führe eine Reduktion mit der Gleichung 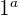 und
und 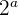 durch, um
durch, um  in der Gleichung
in der Gleichung 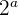 zu eliminieren. Dann setzt du als zweite Gleichung das Ergebnis der Berechnung ein:
zu eliminieren. Dann setzt du als zweite Gleichung das Ergebnis der Berechnung ein:
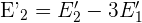
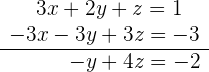
3 Wiederhole das Ganze mit der Gleichung 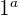 und
und  , um
, um  zu eliminieren.
zu eliminieren.
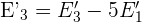


4 Nimm die umgeformten Gleichungen 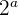 und
und  , zur Reduktion und eliminiere den Term in
, zur Reduktion und eliminiere den Term in  .
.
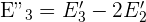
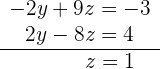
5 Du erhältst das äquivalente Gleichungssystem.
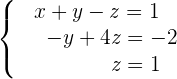
6 Finde die Lösungen.

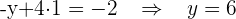
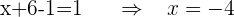
Mit KI zusammenfassen:



