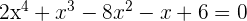
1
Nimm die Divisoren des unabhängigen Terms: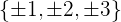 
.
2
Durch die Anwendung des Restsatzes weißt du, für welche Werte die Division exakt ist.
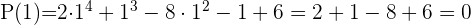
3
Teile durch Ruffini (Synthetische Teilung).
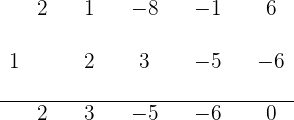
4
Damit die Division exakt ist,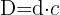 
.
Eine Wurzel ist 
5
Führe nun die gleichen Operationen mit dem zweiten Faktor durch.
6
Versuche es erneut für 
, da der erste Faktor quadriert werden konnte.
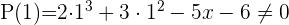
7
Probiere 
aus.
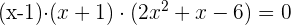
Eine andere Wurzel ist
8
Da das dritte Polynom bereits vom zweiten Grad ist, kannst du es faktorisieren:
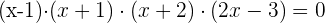
Die Lösungen sind: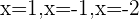 
y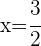 
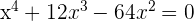
1
Nimm den gemeinsamen Faktor 
heraus.
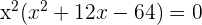
2
Da du ein Produkt gleich Null hast, ist entweder der eine Faktor Null oder der andere Faktor ist Null oder beide sind Null
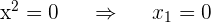
3
Faktorisiere das zweite quadratische Polynom
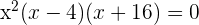
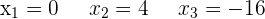
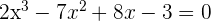
1
Nimm die Divisoren des unabhängigen Terms: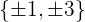 
.
2
Durch die Anwendung des Restsatzes weißt du, für welche Werte die Division exakt ist.
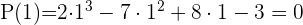
3
Dividiere durch Ruffini
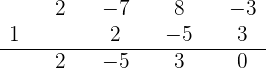
4
Damit es die exakte Division ist,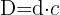
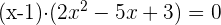
5
Führe nun die gleichen Operationen mit dem zweiten Faktor durch.
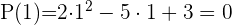
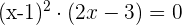
Die Wurzeln sind: 
und 
1
Nimm die Divisoren des unabhängigen Terms: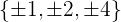 
2
Durch Anwendung des Restsatzes weißt du, für welche Werte die Division exakt ist
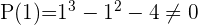
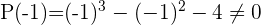
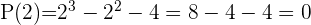
3
Dividiere durch Ruffini.
4
Damit es die exakte Division ist,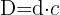
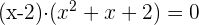
5
Zerlege den zweiten Faktor durch Lösen der quadratischen Gleichung
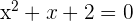
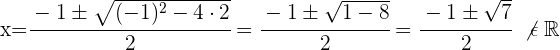
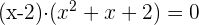
Da die Gleichung keine Lösung hat, gibt es nur eine Wurzel: 
.
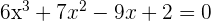
1
Nimm die Divisoren des unabhängigen Terms: 
2
Durch Anwendung des Restsatzes weißt du, für welche Werte die Division exakt ist
P(1) = 6 · 1³ + 7 · 1² − 9 · 1 + 2 ≠ 0
P(−1) = 6 · (−1)³ + 7 · (−1)² − 9 · (−1) + 2 ≠ 0
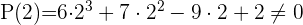
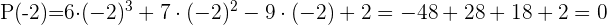
3
Dividiere durch Ruffini
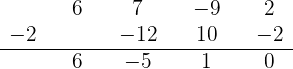
4
Damit es die exakte Division ist,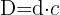
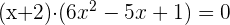
5
Zerlege den zweiten Faktor durch Lösen der quadratischen Gleichung
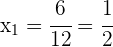
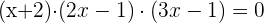
Wurzeln: 
, 
und 
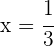
1
Nimm die Divisoren des unabhängigen Terms: {±1, ±2, ±3, ±4, ±6, ±12}
2
Durch Anwendung des Restsatzes weißt du, für welche Werte die Division exakt ist
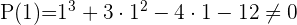
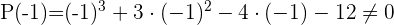
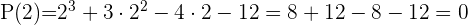
3
Dividiere durch Ruffini.
4
Damit die Division exakt ist, .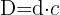
5
Zerlege den zweiten Faktor durch Lösen der quadratischen Gleichung
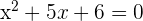
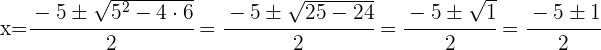
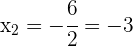
Die Lösungen sind: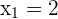 
, 
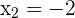und 
.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
