Kapitel

Substitutionsverfahren für Gleichungssysteme
Das Substitutionsverfahren besteht, wie der Name schon sagt, darin, den in einer der Gleichungen erhaltenen Wert einer Variablen zu entfernen und in der anderen Gleichung zu substituieren.
HINWEIS
Wenn ein System mehr Unbekannte (Variablen) als Anzahl der Gleichungenhat, dann hat das System unendlich viele Lösungen, das heißt, jede Variable kann verschiedene Werte annehmen, so dass immer die Gleichung erfüllt ist. Die Anzahl der Werte, die jede Variable annehmen kann, ist unendlich. Beispiel:
Gegeben ist die Gleichung: 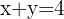 Man stellt fest, dass dies eine Gleichung mit zwei Variablen ist. Man kann schnell einige der Werte herausfinden:
Man stellt fest, dass dies eine Gleichung mit zwei Variablen ist. Man kann schnell einige der Werte herausfinden:
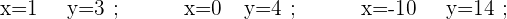

Beachte, dass es eine unendliche Anzahl von Werten gibt, die du  und
und  zuweisen kannst, um sie zu Lösungen zu machen.
zuweisen kannst, um sie zu Lösungen zu machen.
Wenn das System die gleiche Anzahl von Gleichungen und Unbekannten hat, dann hat das System im Allgemeinen nur eine Lösung.
Beispiel für die Vorgehensweise mit einem 2x2-Gleichungsystem
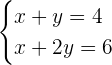
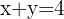 wird "Gleichung I" genannt und
wird "Gleichung I" genannt und
 wird "Gleichung II“ genannt
wird "Gleichung II“ genannt
Entferne eine der beiden Variablen in einer der beiden Gleichungen (du solltest immer diejenige suchen, die weniger algebraische Arbeit erfordert), in diesem Fall eliminierst du  in Gleichung I
in Gleichung I
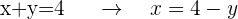
Dies wird als "Wert von  in Bezug auf
in Bezug auf  " bezeichnet
" bezeichnet
Setze den berechneten Wert in die andere Gleichung ein, in diesem Fall setzt du also den Wert von  in Gleichung II ein
in Gleichung II ein
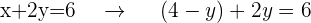
Wie du feststellen kannst, gibt es in der Gleichung jetzt nur noch die Variable  . Diese Gleichung kann vereinfacht und verrechnet werden, um den Wert von
. Diese Gleichung kann vereinfacht und verrechnet werden, um den Wert von  zu erhalten.
zu erhalten.
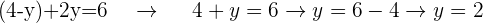
Sobald du den Wert einer der Variablen hast, in diesem Fall  , kannst du ihn in eine der 2 Gleichungen einsetzen, um den Wert der anderen Variablen zu finden, in diesem Fall
, kannst du ihn in eine der 2 Gleichungen einsetzen, um den Wert der anderen Variablen zu finden, in diesem Fall  .
.
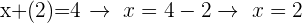
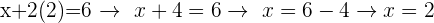
Du kannst auch die andere Gleichung verwenden, da sie dir direkt den Wert von x liefert
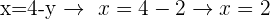
Und so erhältst du den Wert deiner Variablen in einem Gleichungssystem und stellst fest, dass es eine EINZIGE Lösung gibt.
Schritte zum Lösen eines linearen 3x3-Gleichungssystems
1 Wähle eine Variable und eliminiere sie in einer der Gleichungen.
Im Allgemeinen wird die Variable mit dem kleinsten Koeffizienten gewählt, und zwar aus der einfachsten Gleichung, um algebraische Arbeit zu ersparen.
2 Substituiere die beiden anderen Gleichungen.
Nun können diese Variablen in die anderen beiden Gleichungen eingesetzt werden. Die beiden neuen Gleichungen, die sich aus diesem Schritt ergeben, bilden ein 2x2-Gleichungssystem.
3 Löse das 2x2-Gleichungssystem.
Hierfür wiederholst du den Vorgang:
- Wähle eine der 2 Variablen aus und eliminiere sie in einer der Gleichungen.
- Setze nun die Variable in die andere Gleichung ein (diejenige, die man im 2x2-Gleichungssystem nicht verwendet hat).
- Aus dem vorherigen Schritt erhältst du eine lineare Gleichung mit einer Variablen, und wenn du diese eliminierst, erhältst du ihren Wert.
- Ersetze den erhaltenen Wert in diesem 2x2-Gleichungssystem und berechne den Wert einer anderen Variablen.
4 Erhalte den Wert der fehlenden Variablen
Wie bei Schritt 3 erhältst du den Wert von zwei der drei Variablen. Um die fehlende dritte Variable zu erhalten, verwendest du Schritt 1 und ersetzt sie durch die Unbekannten, die du bereits gelöst hast.
Übungen zu 3x3 Gleichungssystemen
1

Um das Substitutionsverfahren anzuwenden, musst du eine Gleichung und eine Variable auswählen, die du eliminieren möchtest. Wähle nun die dritte Gleichung, da sie diejenige mit dem kleinsten Koeffizienten in der Variablen ist 

Setze das Ergebnis dann in die anderen 2 Gleichungen ein






Daraus ergibt sich ein neues 2x2-Gleichungssystem

Nun musst du wieder das Substitutionsverfahren anwenden, d. h. eine Gleichung und eine Variable zum Eliminieren wählen. Am einfachsten ist in diesem Fall die erste Gleichung mit der Variablen  .
.

Setze das Ergebnis dann in die andere Gleichung ein




Da du bereits z=1 kennst, verwendest du die zuletzt berechnete Gleichung, um y zu finden

Setze zuletzt die beiden berechneten Variablen in die erste Gleichung ein, in diesem Fall 
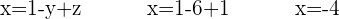
2

Um das Substitutionsverfahren anzuwenden, musst du eine Gleichung und eine Variable auswählen, die du eliminieren möchtest. Wähle nun die zweite Gleichung, da sie diejenige mit dem kleinsten Koeffizienten in der Variablen ist 

Setze das Ergebnis dann in die anderen 2 Gleichungen ein






Daraus ergibt sich ein neues 2x2-Gleichungssystem
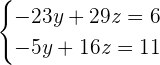
Wende nun wieder das Substitutionsverfahren an, d. h. wähle eine Gleichung und eine Variable zum Eliminieren aus. Am einfachsten ist in diesem Fall die zweite Gleichung mit der Variablen  .
.
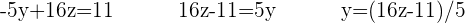
Setze das Ergebnis dann in die andere Gleichung ein. Um den Nenner loszuwerden, musst die gesamte Gleichung mit 5 multiplizieren





Da du bereits  kennst, nutzt du die zuletzt verwendete Gleichung
kennst, nutzt du die zuletzt verwendete Gleichung
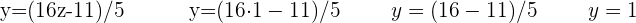
Setze zuletzt die beiden berechneten Variablen in die erste Gleichung ein, in diesem Fall 

3 

Um das Substitutionsverfahren anzuwenden, musst du eine Gleichung und eine Variable auswählen, die du eliminieren möchtest. Wähle nun die erste Gleichung, also diejenige mit dem kleinsten Koeffizienten in der Variablen 

Setze das Ergebnis dann in die anderen 2 Gleichungen ein






Daraus ergibt sich ein neues 2x2-Gleichungssystem
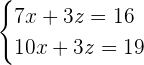
Wende nun wieder das Substitutionsverfahren an, d. h. wähle eine Gleichung und eine Variable zum Eliminieren aus. Am einfachsten ist in diesem Fall die erste Gleichung mit der Variablen  .
.

Setze das Ergebnis dann in die andere Gleichung ein







Da du bereits  kennst, verwendest du die zuletzt verwendete Gleichung um
kennst, verwendest du die zuletzt verwendete Gleichung um  finden
finden

Setze zuletzt die beiden berechneten Variablen in die erste Gleichung ein, in diesem Fall 
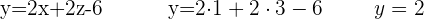
Allgemeine Probleme, die mit Gleichungssystemen gelöst werden
1 Ein Supermarktkunde hat für  Milch,
Milch,  Schinken und
Schinken und  Olivenöl insgesamt
Olivenöl insgesamt  € bezahlt. Berechne den Preis der einzelnen Artikel. Du weißt, dass
€ bezahlt. Berechne den Preis der einzelnen Artikel. Du weißt, dass  Öl dreimal so viel wie
Öl dreimal so viel wie  Milch kostet
Milch kostet
und dass  Schinken das Gleiche kostet wie
Schinken das Gleiche kostet wie  Öl plus
Öl plus  Milch.
Milch.
Milch: 
Schinken: 
Olivenöl: 
Jeder Satz der Aufgabenstellung ergibt eine Gleichung, die das folgende lineare Gleichungssystem bildet

In diesem Fall haben zwei der Gleichungen bereits eliminierte Variablen (Gleichung 2 und 3). Setze nun den Wert von  aus der zweiten Gleichung in die dritte Gleichung ein.
aus der zweiten Gleichung in die dritte Gleichung ein.
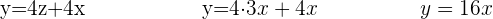
Setze anschließend den Wert von  und von
und von  in die erste Gleichung ein
in die erste Gleichung ein





Verwende die Ergebnisse von  und von
und von  um ihren Wert zu erhalten
um ihren Wert zu erhalten

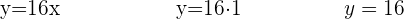
Du erhälst:
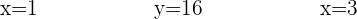
Das heißt, die Preise betragen
Milch: 1 €
Schinken: 16 €
Olivenöl: 3 €
2 Eine Videothek ist auf drei Arten von Filmen spezialisiert:
- Kinderfilme
- Amerikanische Western
- Terrorfilme
Es ist bekannt, dass:
 der Kinderfilme plus
der Kinderfilme plus  der Western
der Western  der Gesamtzahl der Filme ausmachen.
der Gesamtzahl der Filme ausmachen.
 der Kinderfilme plus
der Kinderfilme plus  der Western plus
der Western plus  der Terrorfilme machen die Hälfte der Gesamtzahl der Filme aus.
der Terrorfilme machen die Hälfte der Gesamtzahl der Filme aus.
Es gibt  mehr Western als Kinderfilme.
mehr Western als Kinderfilme.
Ermittle die Anzahl der Filme von jedem Typ.
Kinderfilme: 
Amerikanische Western: 
Terrorfilme: 
Aus dem Wortlaut der Aufgabenstellung erhältst du das 3x3-Gleichungssystem

Erstelle die erste Gleichung und vereinfache sie

Multipliziere die gesamte Gleichung mit 100, um den einfachen Nenner loszuwerden und um die erhaltene Gleichung zu vereinfachen:



Du teilst durch  und erhältst:
und erhältst:

Nimm die zweite Gleichung und verfolge die gleichen Schritte:

Um den gleichen gemeinsamen Nenner zu haben, multiplizierst du die Brüche auf der rechten Seite mit  und erhälst:
und erhälst:

Lass den Nenner weg und vereinfache:


Teile die Gleichung durch  und erhalte:
und erhalte:

Unter Verwendung der vereinfachten Versionen der ersten und zweiten Gleichung erstellst du dann das folgende Gleichungssystem:

Da du bereits eine Variable in einer der Gleichungen eliminiert hast, verwendest du sie, um den Wert von  in den beiden Ausgangsgleichungen zu ersetzen und die letzte erhaltene mit 3 zu multiplizieren.
in den beiden Ausgangsgleichungen zu ersetzen und die letzte erhaltene mit 3 zu multiplizieren.






Daraus ergibt sich ein neues 2x2-Gleichungssystem

Nun musst du wieder das Substitutionsverfahren anwenden, d. h. eine Gleichung und eine Variable zum Eliminieren wählen. Am einfachsten ist in diesem Fall die zweite Gleichung mit der Variablen  .
.

Das Ergebnis fügst du dann in die andere Gleichung ein





Da du bereits  kennst, verwendest du die zuletzt verwendete Gleichung um
kennst, verwendest du die zuletzt verwendete Gleichung um  zu finden
zu finden

Verwende jetzt die erste Gleichung für die Variable, die noch fehlt, in diesem Fall 
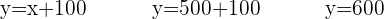
Abschließend stellst du folgendes fest. Es gibt:
500 Kinderfilme
600 Westernfilme
900 Terrorfilme
3 Die Seiten eines Dreiecks messen  ,
,  und
und  .
.
Mit dem Mittelpunkt in jedem Scheitelpunkt werden drei Kreise gezeichnet, die sich jeweils zu zweit berühren.
Berechne die Längen der Radien der Kreise.
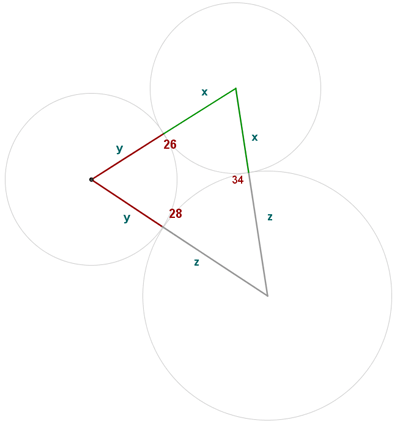
Aus der Skizze der Abbildung und der Verwendung einer Variablen für jeden Radius der 3 Kreise ergibt sich das Gleichungssystem

Um das Substitutionsverfahren anzuwenden, musst du eine Gleichung und eine Variable auswählen, die du eliminieren möchtest. In diesem Fall eliminierst du am besten die Variable  aus der ersten Gleichung
aus der ersten Gleichung

Setze das Ergebnis dann in die anderen 2 Gleichungen ein



In diesem Fall hat die Gleichung keine Variable x, also lässt du sie einfach stehen.
Daraus ergibt sich ein neues 2x2-Gleichungssystem

Nun musst du wieder das Substitutionsverfahren anwenden, d. h. eine Gleichung und eine Variable zum Eliminieren wählen. Am einfachsten ist in diesem Fall die zweite Gleichung mit der Variablen  .
.

Füge das Ergebnis dann in die andere Gleichung ein






Da du bereits  kennst, nutzt du die zuletzt verwendete Gleichung um
kennst, nutzt du die zuletzt verwendete Gleichung um  zu finden
zu finden
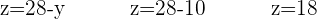
Verwende nun die erste Gleichung für die Variable, die noch fehlt, in diesem Fall 
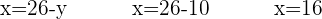
Mit KI zusammenfassen:






















