
Was ist eine Gleichung höheren Grades?
Eine Gleichung höheren Grades ist eine Gleichung, die wie folgt geschrieben wird:

wobei 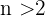
Diese Art von Gleichung kann in lineare und quadratische Faktoren zerlegt werden. Dann genügt es, jeden der Faktoren auf Null zu setzen und die resultierenden linearen und quadratischen Gleichungen zu lösen.
Schritte zum Lösen einer Gleichung höheren Grades
Schaue dir am Besten das folgende Beispiel an, um die Auflösungsschritte besser zu verstehen: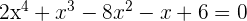
Verwende die Ruffini-Regel und die abc-Formel für quadratische Gleichungen, um die Gleichung zu vereinfachen.
I - Faktorisiere die Gleichung vierten Grades
Um die Gleichung 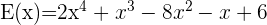 zu faktorisieren
zu faktorisieren
1 Suche nach den Divisoren des unabhängigen Terms.
Der unabhängige Term ist  , da der unabhängige Term eines Polynoms derjenige ist, der nicht mit
, da der unabhängige Term eines Polynoms derjenige ist, der nicht mit  multipliziert wird.
multipliziert wird.
Die Teiler von  sind:
sind: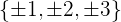 .
.
Du tust dies, um einen Wert zu finden, der die Gleichung  , löst, und somit eine Wurzel der Gleichung zu finden, damit es einfacher ist, sie zu faktorisieren. Sobald die Teiler des unabhängigen Terms gefunden sind, ist der nächste Schritt:
, löst, und somit eine Wurzel der Gleichung zu finden, damit es einfacher ist, sie zu faktorisieren. Sobald die Teiler des unabhängigen Terms gefunden sind, ist der nächste Schritt:
2 Werte das Polynom in den Divisoren des unabhängigen Terms aus.
Wenn 
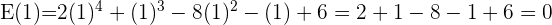
 , ist daher eine Wurzel aus
, ist daher eine Wurzel aus 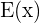 .
.
Da du eine Wurzel gefunden hast, weißt du, dass der Term 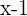 die Gleichung
die Gleichung 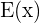 dividiert.
dividiert.
3 Verwende die Ruffini-Regel.
Mit der Ruffini-Regel ist es einfach, die Division von 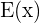 durch
durch 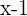 zu berechnen.
zu berechnen.
Nimmst du die Terme von 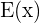 , die gefundene Wurzel
, die gefundene Wurzel  und platzierst sie so, wie es die Ruffini-Regel vorgibt, so erhältst du:
und platzierst sie so, wie es die Ruffini-Regel vorgibt, so erhältst du:
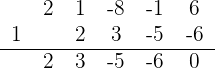
Dies impliziert, dass die Division von 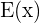 durch die Wurzel
durch die Wurzel  die Gleichung
die Gleichung 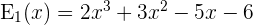 ergibt.
ergibt.
Es gilt also 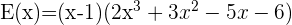 .
.
II - Faktorisiere die Gleichung dritten Grades
Um die im vorherigen Schritt erhaltene Gleichung 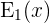 zu faktorisieren, wird ein ähnliches Verfahren verwendet.
zu faktorisieren, wird ein ähnliches Verfahren verwendet.
1Prüfe, ob sich die Zahl  als wiederholte Wurzel erweist, d. h., dass
als wiederholte Wurzel erweist, d. h., dass  auch eine Lösung der Gleichung
auch eine Lösung der Gleichung 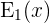 ist, und werte aus:
ist, und werte aus:

Du verstehst, dass  keine sich wiederholende Wurzel ist.
keine sich wiederholende Wurzel ist.
2Prüfe, ob die verbleibenden Teiler des unabhängigen Terms der ursprünglichen Gleichung 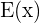 Wurzeln von
Wurzeln von 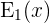 sind.
sind.
Du stellst fest, dass mit  Folgendes gilt:
Folgendes gilt:

Daher ist  eine Wurzel von
eine Wurzel von  .
.
Das heißt:  teilt
teilt 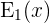 .
.
3Verwende die Ruffini-Regel um 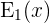 durch
durch  zu teilen.
zu teilen.
Nimm die Wurzel, die du in diesem Schritt gefunden hast  und die Koeffizienten von
und die Koeffizienten von 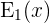 , um sie auf folgende Weise zu ordnen und erhalten:
, um sie auf folgende Weise zu ordnen und erhalten:

Dies impliziert, dass das Ergebnis der Division der Ausdruck  ist.
ist.
Das heißt, dass  ist.
ist.
Daher musst du im Gegenzug: 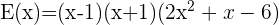 .
.
III - Faktorisiere die quadratische Gleichung
Dieser Schritt ist recht einfach, da du nur die Wurzeln des Polynoms vom Grad 
 finden musst..
finden musst..
Du kannst diese Wurzeln leicht mit der abc-Formel für quadratische Gleichungen berechnen:

Dann sind die Wurzeln von  :
:
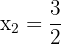 .
.
Dies impliziert, dass 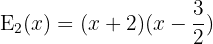 .
.
Daraus kannst du schließen, dass: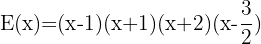 .
.
Lösungen

Faktorisierung
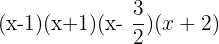
Mit KI zusammenfassen:













