Rationale Gleichungen sind Gleichungen, in denen Polynombrüche vorkommen.
Lösen von rationalen Gleichungen
Um gebrochene oder rationale Gleichungen zu lösen, multiplizierst du beide Glieder der Gleichung mit dem kleinsten gemeinsamen Vielfachen der Nenner.
Überprüfe die Lösungen, um mögliche seltsame Lösungen auszuschließen, die aus der umgewandelten Gleichung stammen (die sich aus der Multiplikation mit dem kleinsten gemeinsamen Vielfachen ergibt), die aber nicht aus der ursprünglichen Gleichung stammen.
Beispiel für das Lösen von rationalen Gleichungen
1
Bringe alles auf einen gemeinsamen Nenner. Dazu berechnest du den Mittelwert der Nenner:
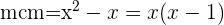
Dividiere den Effektivwert durch jeden Nenner und multiplizierst das Ergebnis mit dem entsprechenden Zähler
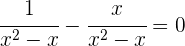
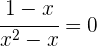
Du erhältst den Nenner, indem du mit dem, was übrig bleibt, multiplizierst:
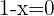
Eliminiere die Variable 
Prüfe die Lösung
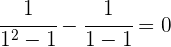
Die Gleichung hat keine Lösung für weil sich die Nenner aufheben, es gibt keinen Bruch mit Null-Nenner
2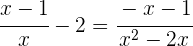
Berechne das kleinste gemeinsame Vielfache der Nenner:
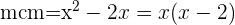
Dividiere den Effektivwert durch jeden Nenner und multipliziere das Ergebnis mit dem entsprechenden Zähler
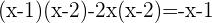
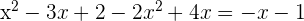
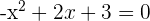
Löse die resultierende quadratische Gleichung
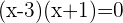
Prüfe die Lösungen:
Für
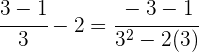
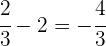
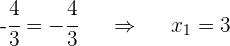ist eine Lösung der Gleichung.
Für
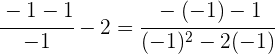
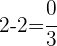
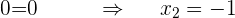ist eine Lösung der Gleichung.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
