Biquadratische Gleichungen sind Gleichungen vierten Grades, die keine ungeraden Exponenten enthalten:
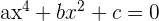
Lösen von biquadratischen Gleichungen
Um biquadratische Gleichungen zu lösen, nimmst du die Variablenänderung (Substitution) mit 
vor:
Für jeden positiven Wert von gibt es zwei Werte von 
:
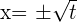
Beispiele
1
Nimm die Änderung der Variablen (Substitution)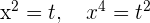 
vor und du erhältst:
Löse nun die obige Gleichung und du erhältst:
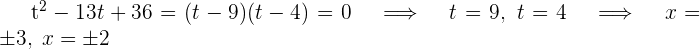
Diese biquadratische Gleichung hat also vier reelle Lösungen:
2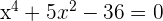
Nimm die Änderung der Variablen 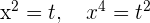vor und du erhältst:
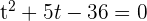
Löse nun die obige Gleichung (Resubstitution) und du erhältst
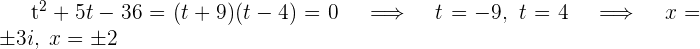
Diese biquadratische Gleichung hat zwei reelle und zwei komplexe Lösungen.
3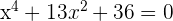
Nimm die Änderung der Variablen (Substitution) 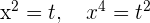vor und du erhältst
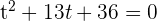
Löse nun die obige Gleichung (Resubstitution) und du erhältst
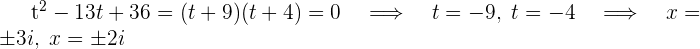
Diese biquadratische Gleichung hat keine reellen Lösungen, sie hat vier komplexe Lösungen.
Andere Gleichungen mit Variablenänderung
Das gleiche Verfahren kann verwendet werden, um Gleichungen folgender Form zu lösen:
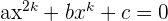
Führe mit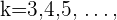 
die Variablenänderung (Substitution) durch:
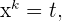
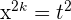
Beispiel:
Löse die Gleichung
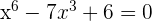
Nimm die Änderung der Variablen (Substitution)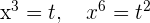 
vor und du erhältst
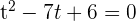
Löse nun die obige Gleichung (Resubstitution) und du erhältst:
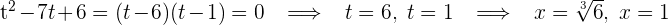
Diese biquadratische Gleichung hat zwei reelle Lösungen.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
