Kapitel

Gleichungssysteme mit eindeutiger Lösung
Löse die folgenden Gleichungssysteme mit der grafischen Methode.
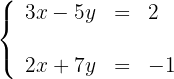
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wenn wir den Schnittpunkt mit den Achsen berücksichtigen. Für die erste Gerade haben wir
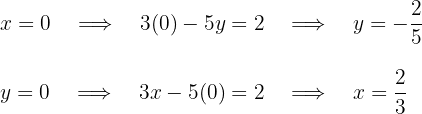 Die Schnittpunkte der ersten Geraden mit den Achsen sind
Die Schnittpunkte der ersten Geraden mit den Achsen sind  Die Schnittpunkte der zweiten Geraden mit den Achsen sind
Die Schnittpunkte der zweiten Geraden mit den Achsen sind 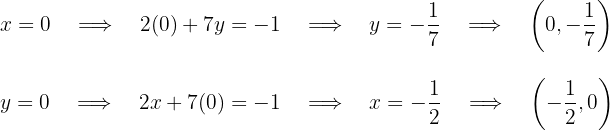
Wir verwenden die Schnittpunkte mit den Achsen als Punkte, um die Gerade zu zeichnen. Du kannst aber zwei beliebige Werte von  nehmen und die Werte von
nehmen und die Werte von  erhalten; Dann zeichnest du mit einem Lineal die Gerade durch beide Punkte. Die Gerade, die du erhältst, ist dieselbe wie die, die wir vorgestellt haben.
erhalten; Dann zeichnest du mit einem Lineal die Gerade durch beide Punkte. Die Gerade, die du erhältst, ist dieselbe wie die, die wir vorgestellt haben.
2Wir stellen die Schnittpunkte mit den Achsen in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden
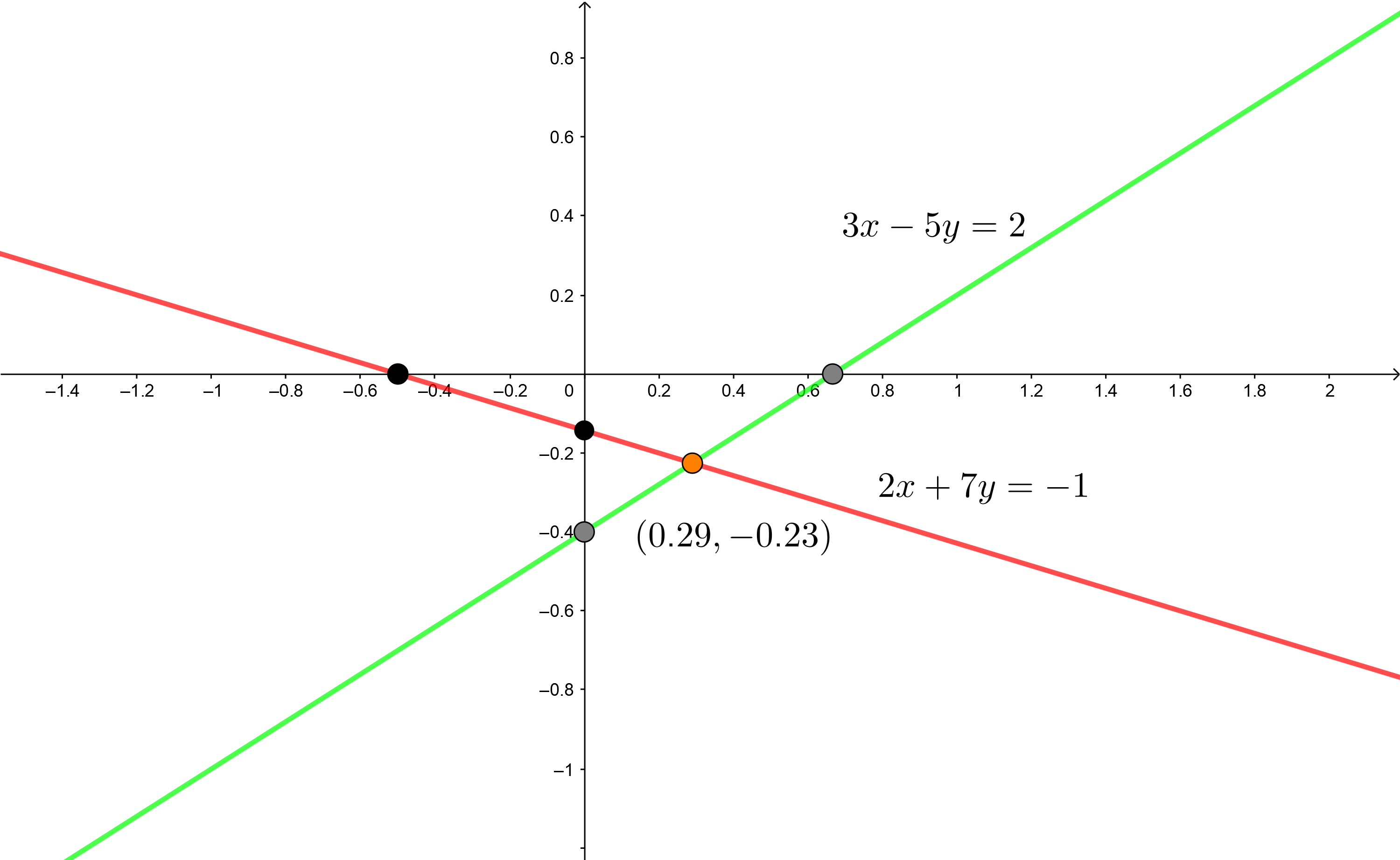
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 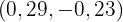 . Man beachte, dass die Gleichheit nicht erfüllt ist, wenn wir unsere Lösung in beide Gleichungen einsetzen.
. Man beachte, dass die Gleichheit nicht erfüllt ist, wenn wir unsere Lösung in beide Gleichungen einsetzen.
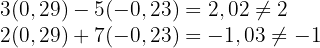
Allerdings liegen sie ziemlich nahe beieinander; dies ist die Schwierigkeit bei der grafischen Methode.
Um exakte Lösungen zu erhalten, werden u.a. die analytischen Methoden der Gleichsetzung, des Addtionsverfahrens, der Substitution usw. verwendet. Unter Verwendung analytischer Methoden lautet das genaue Ergebnis 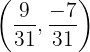
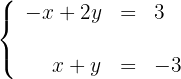
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wenn wir den Schnittpunkt mit den Achsen berücksichtigen. Für die erste Gerade haben wir
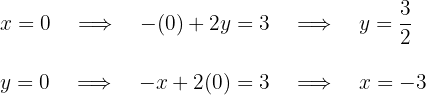 Die Schnittpunkte der ersten Geraden mit den Achsen sind
Die Schnittpunkte der ersten Geraden mit den Achsen sind 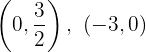 Die Schnittpunkte der zweiten Geraden mit den Achsen sind
Die Schnittpunkte der zweiten Geraden mit den Achsen sind 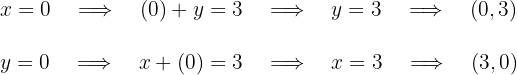
2Wir stellen die Schnittpunkte mit den Achsen in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
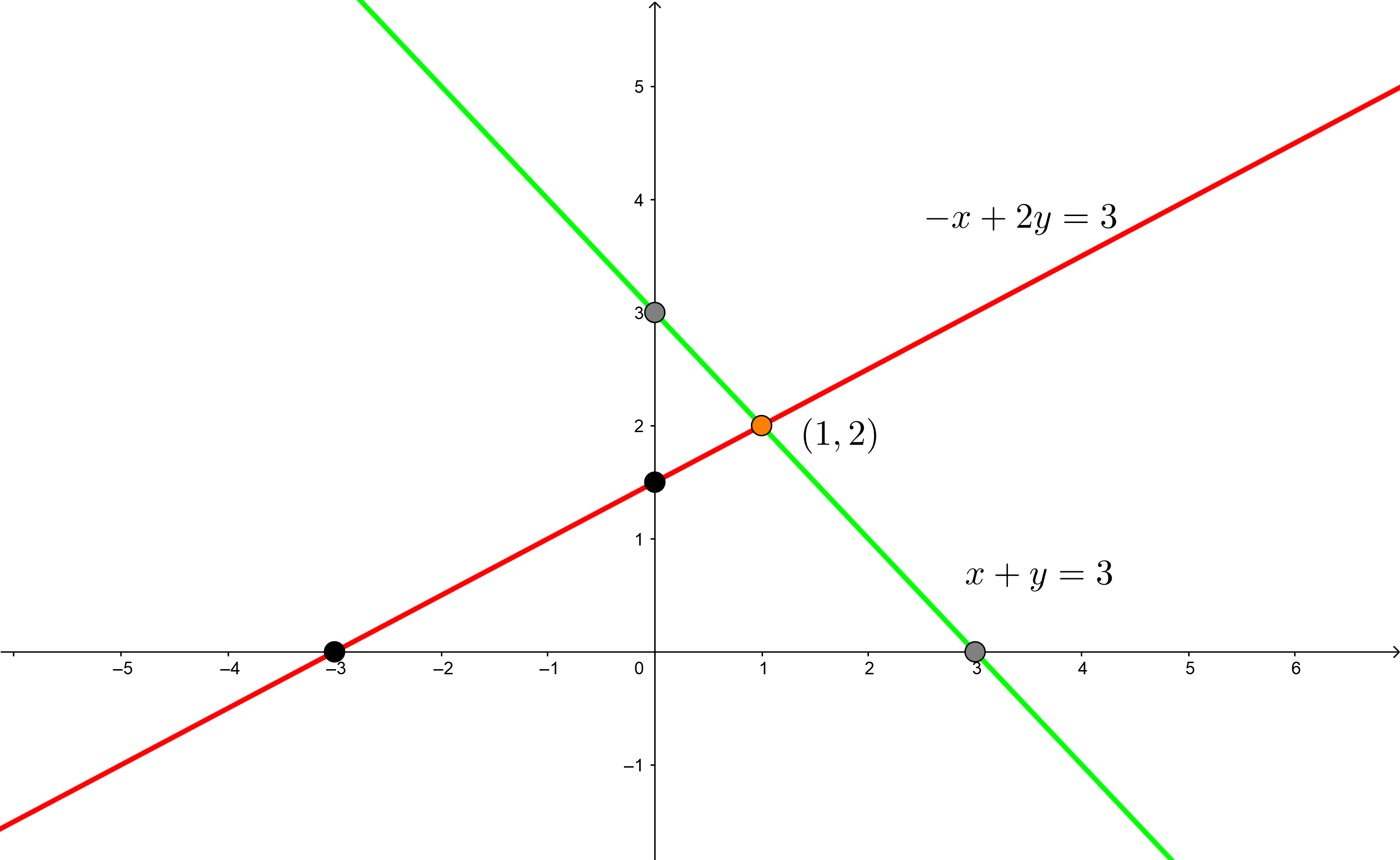
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 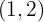 . Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist, so dass die erhaltene Lösung exakt ist
. Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist, so dass die erhaltene Lösung exakt ist
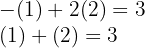
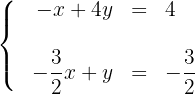
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wenn wir den Schnittpunkt mit den Achsen berücksichtigen. Für die erste Gerade haben wir
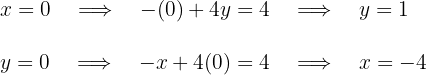 Die Schnittpunkte der ersten Geraden mit den Achsen sind
Die Schnittpunkte der ersten Geraden mit den Achsen sind 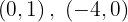 Die Schnittpunkte der zweiten Geraden mit den Achsen sind
Die Schnittpunkte der zweiten Geraden mit den Achsen sind 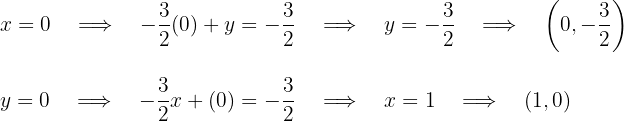
2Wir stellen die Schnittpunkte mit den Achsen in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
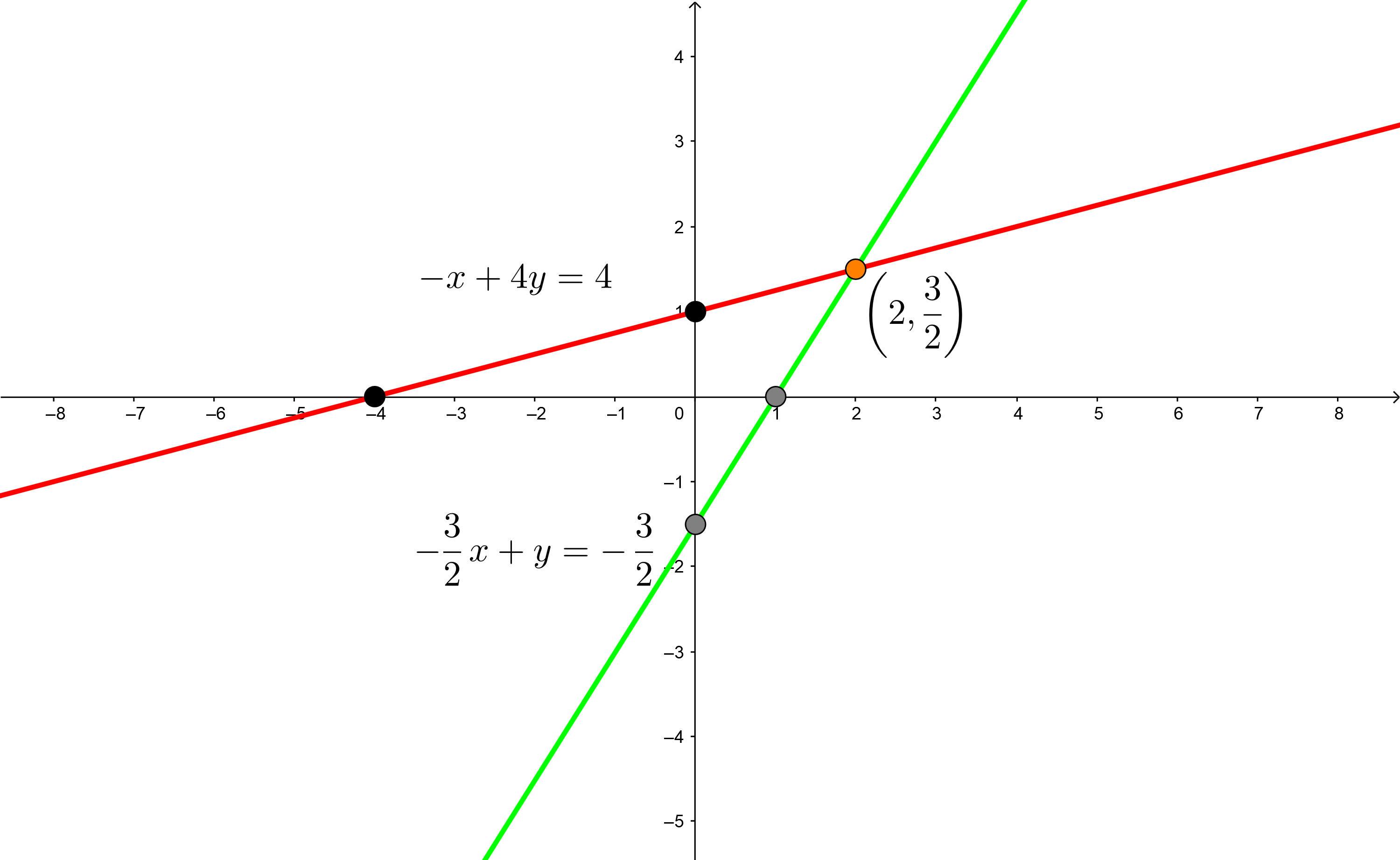
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 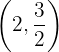 . Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist, so dass die erhaltene Lösung exakt ist
. Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist, so dass die erhaltene Lösung exakt ist
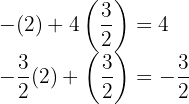
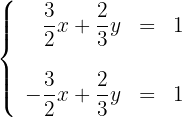
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wobei die Werte 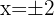 auf beiden Geraden berücksichtigt werden. Für die erste Gerade haben wir
auf beiden Geraden berücksichtigt werden. Für die erste Gerade haben wir
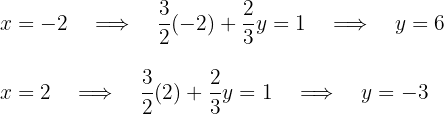 Für die erste Gerade lauten die Punkte
Für die erste Gerade lauten die Punkte 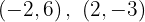 Für die zweite Gerade lauten die Punkte
Für die zweite Gerade lauten die Punkte 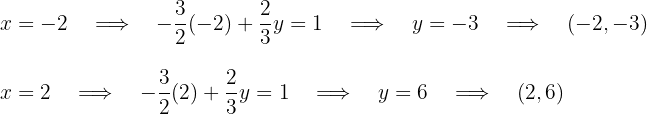
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
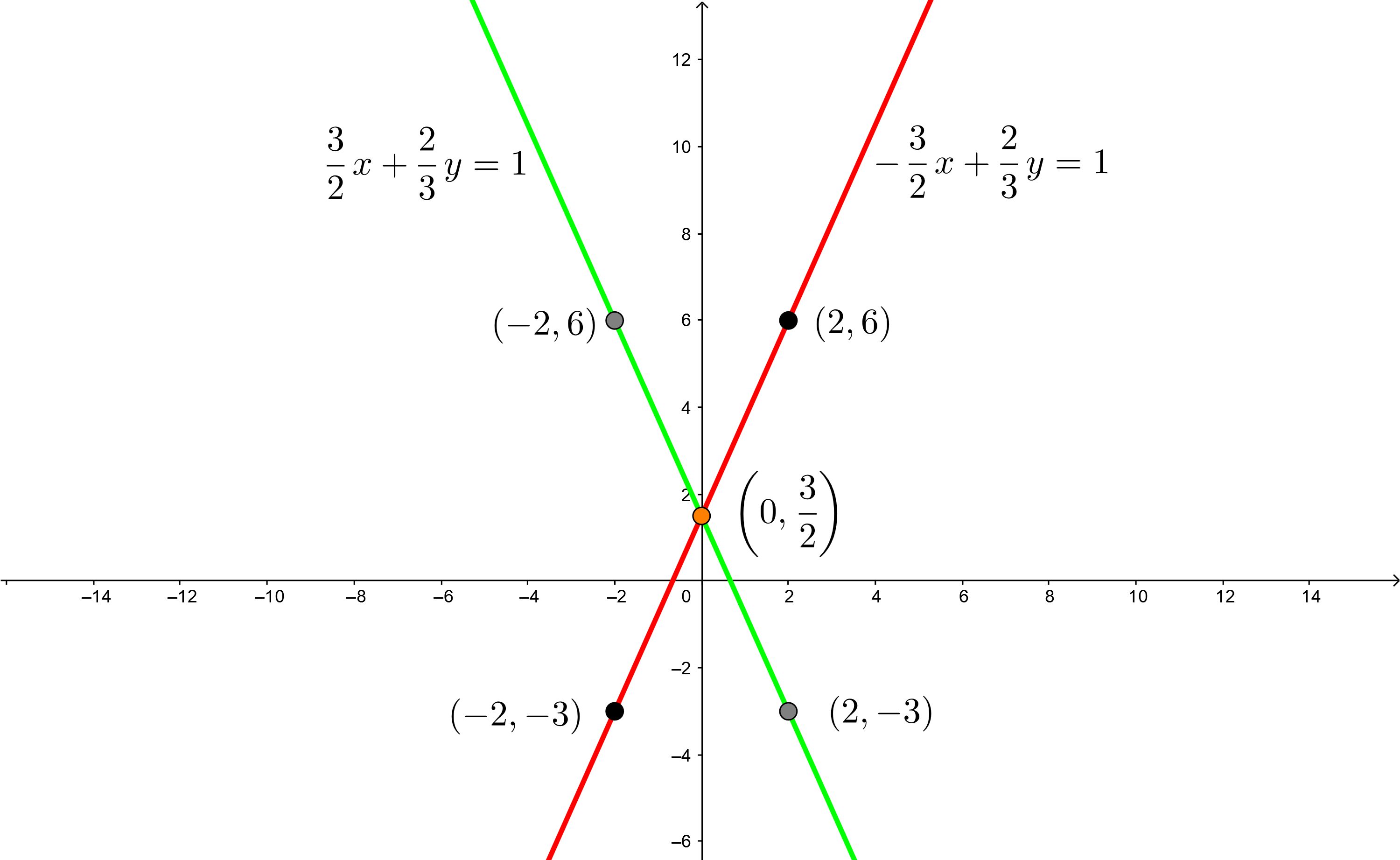
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 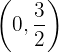 . Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
. Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
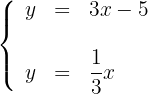
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wenn wir die Werte 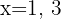 auf der ersten Geraden berücksichtigen. Wir erhalten
auf der ersten Geraden berücksichtigen. Wir erhalten
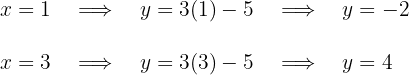 Für die erste Gerade lauten die Punkte
Für die erste Gerade lauten die Punkte 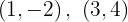 Für die zweite Gerade nehmen wir die Werte
Für die zweite Gerade nehmen wir die Werte 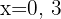 , die erhaltenen Punkte lauten
, die erhaltenen Punkte lauten 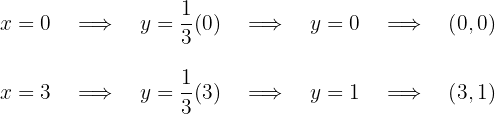
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
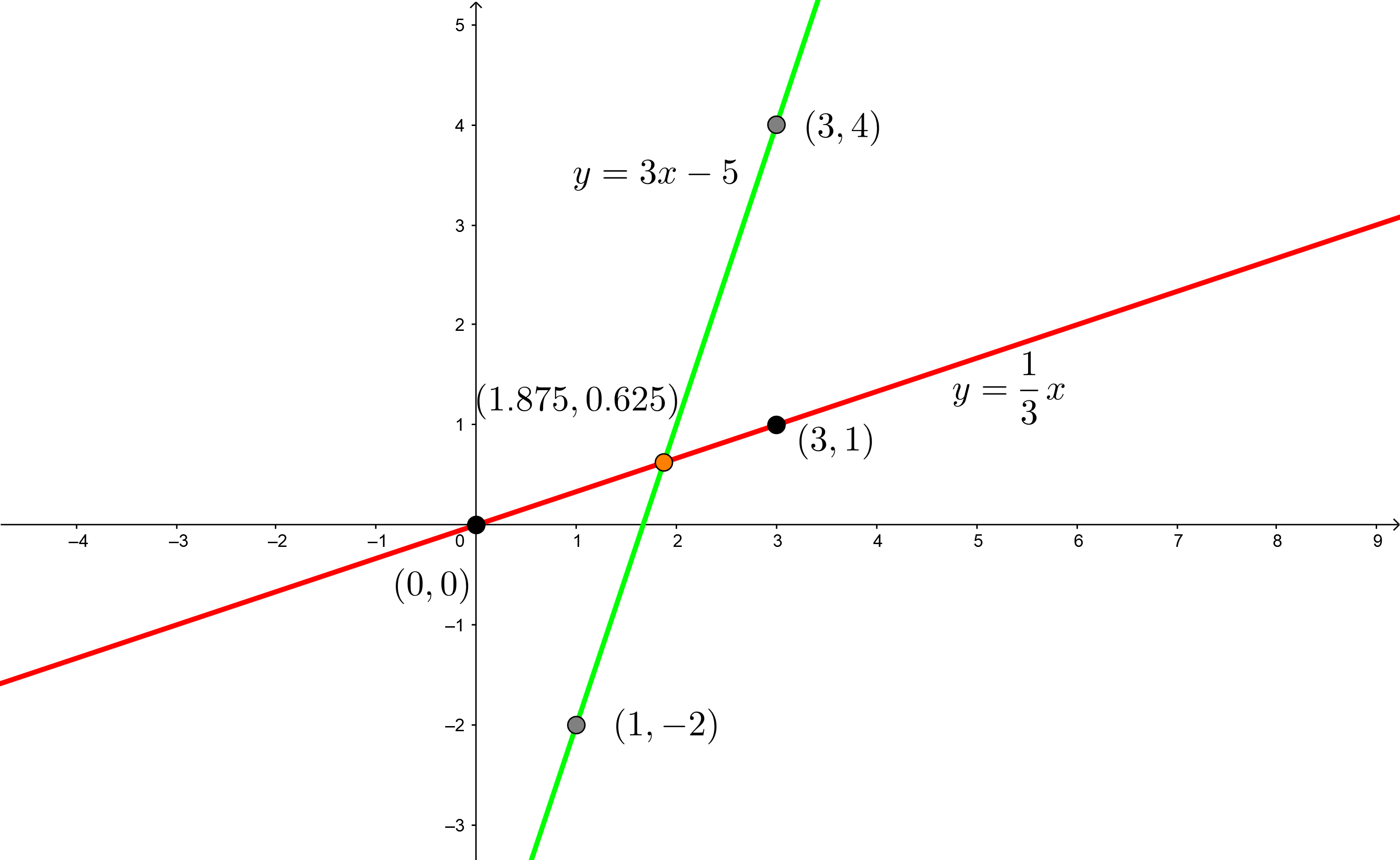
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 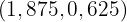 . Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
. Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
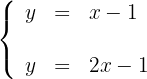
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Linie zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden, wobei die Werte 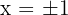 auf beiden Geraden berücksichtigt werden. Für die erste Gerade haben wir
auf beiden Geraden berücksichtigt werden. Für die erste Gerade haben wir
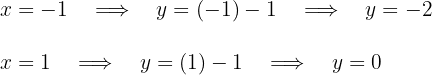 Für die erste Gerade lauten die Punkte
Für die erste Gerade lauten die Punkte 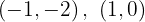 Für die zweite Gerade lauten die Punkte
Für die zweite Gerade lauten die Punkte 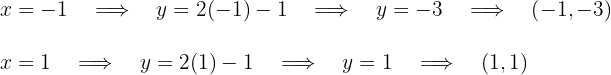
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
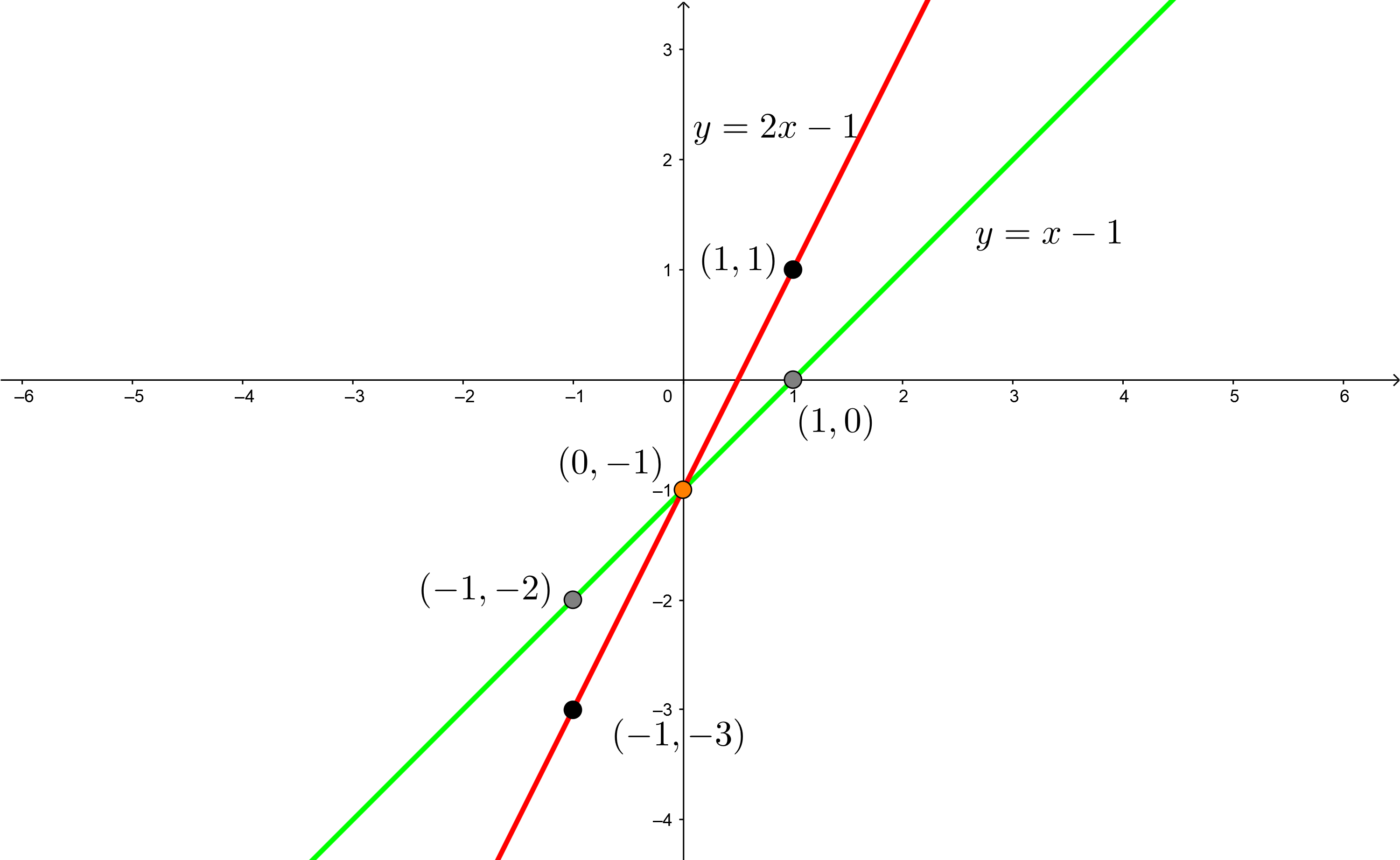
3Die Lösung des Gleichungssystems befindet sich dort, wo sich die beiden Geraden schneiden, d. h., 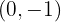 . Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
. Man beachte, dass in diesem Fall, wenn wir unsere Lösung in beide Gleichungen einsetzen, die Gleichheit erfüllt ist.
Gleichungssysteme ohne Lösung
Löse die folgenden Gleichungssysteme mit der grafischen Methode.
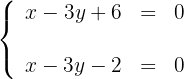
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Gerade zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden. Wenn wir die Werte 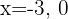 auf der ersten Geraden berücksichtigen, erhalten wir
auf der ersten Geraden berücksichtigen, erhalten wir
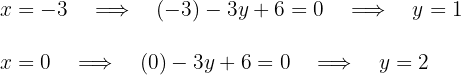 Für die erste Gerade lauten die Punkte
Für die erste Gerade lauten die Punkte 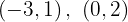 Für die zweite Gerade, wenn wir die Werte
Für die zweite Gerade, wenn wir die Werte 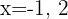 nehmen, lauten die Punkte
nehmen, lauten die Punkte 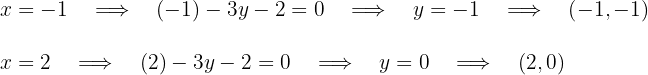
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
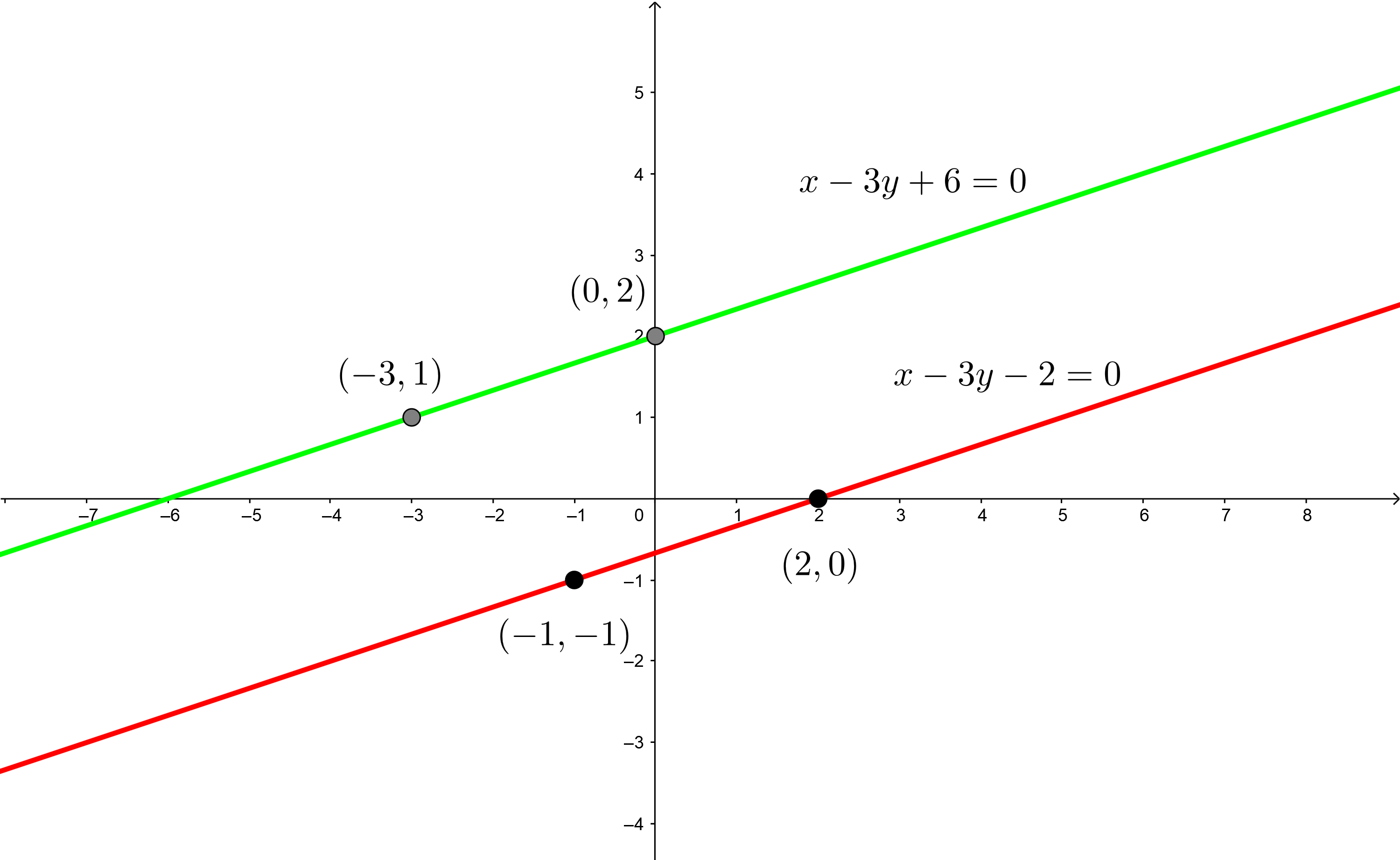
3Das Gleichungssystem ist nicht lösbar, da beide Geraden parallel zueinander verlaufen und es keinen Schnittpunkt gibt, wie aus der Grafik ersichtlich ist. Aus analytischer Sicht haben beide Geraden dieselbe Steigung 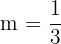 .
.
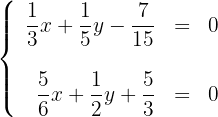
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Gerade zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden. Wir können die Schnittpunkte mit den Achsen finden oder  beliebige Werte zuweisen, um Werte für
beliebige Werte zuweisen, um Werte für  zu erhalten. Hier nehmen wir die Werte
zu erhalten. Hier nehmen wir die Werte 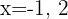 für die erste Gerade
für die erste Gerade
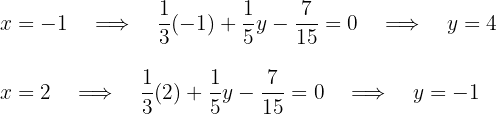 Für die erste Gerade lauten die Punkte
Für die erste Gerade lauten die Punkte 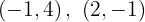 Für die zweite Gerade, wenn wir die Werte
Für die zweite Gerade, wenn wir die Werte 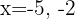 , nehmen, lauten die Punkte
, nehmen, lauten die Punkte 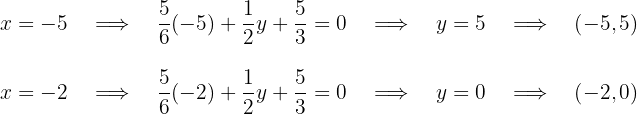
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden.
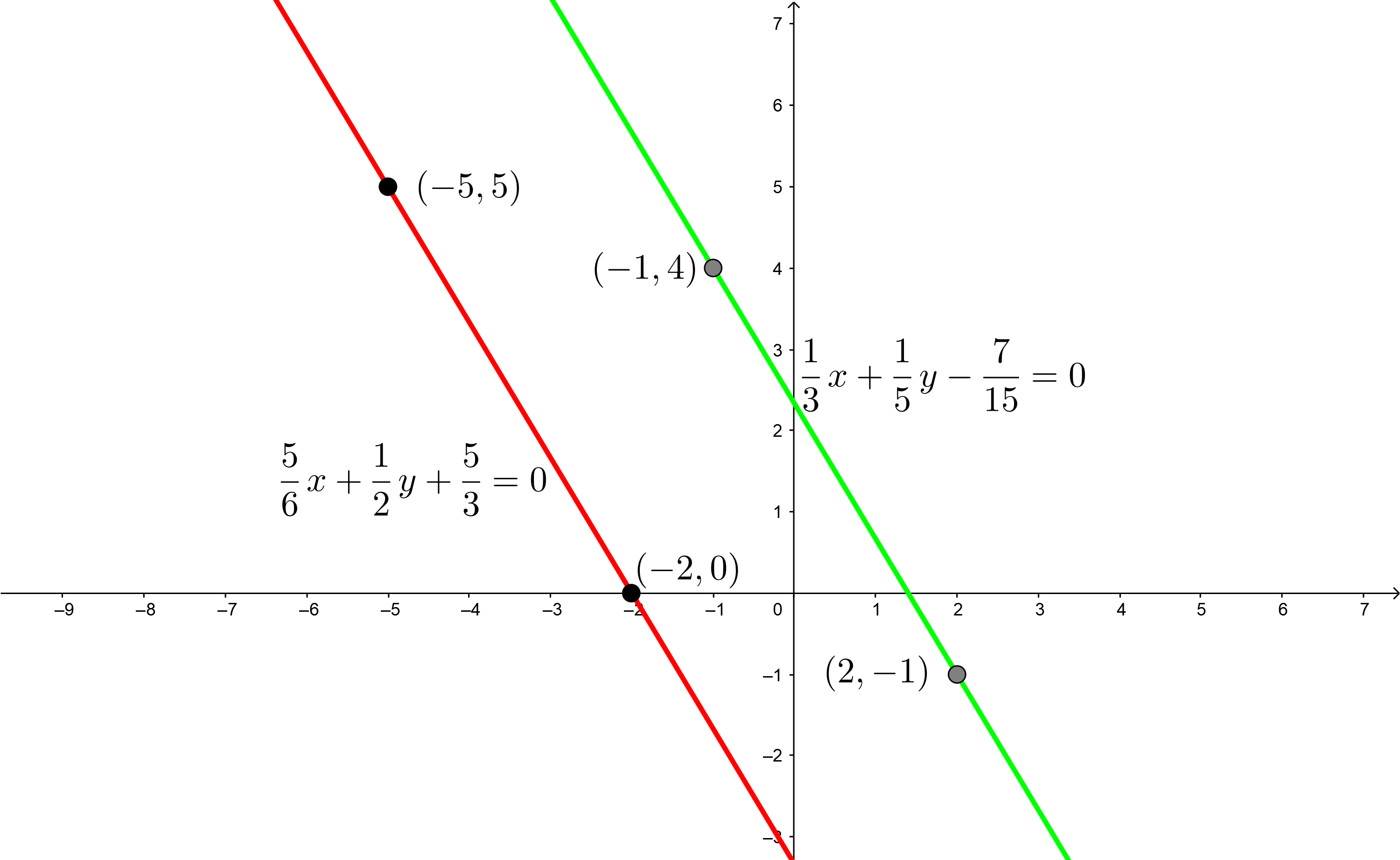
3Das Gleichungssystem ist nicht lösbar, da beide Geraden parallel zueinander verlaufen und es keinen Schnittpunkt gibt, wie aus der Grafik ersichtlich ist. Aus analytischer Sicht haben beide Geraden dieselbe Steigung 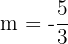 .
.
Gleichungssysteme mit unendlich vielen Lösungen
Löse die folgenden Gleichungssysteme mit der grafischen Methode.
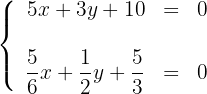
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Gerade zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden. Wir können die Schnittpunkte mit den Achsen finden oder  beliebige Werte zuweisen, um Werte für
beliebige Werte zuweisen, um Werte für  zu erhalten. Hier nehmen wir die Werte
zu erhalten. Hier nehmen wir die Werte 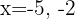 für die erste Gleichung
für die erste Gleichung
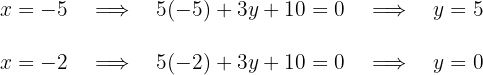 Für die erste Gleichung lauten die Punkte
Für die erste Gleichung lauten die Punkte 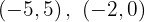 Für die zweite Gleichung, wenn wir die Werte
Für die zweite Gleichung, wenn wir die Werte 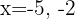 nehmen, lauten die Punkte
nehmen, lauten die Punkte 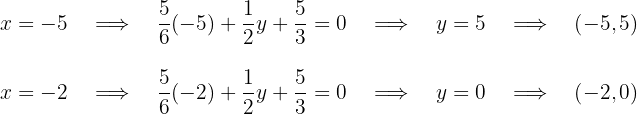
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden
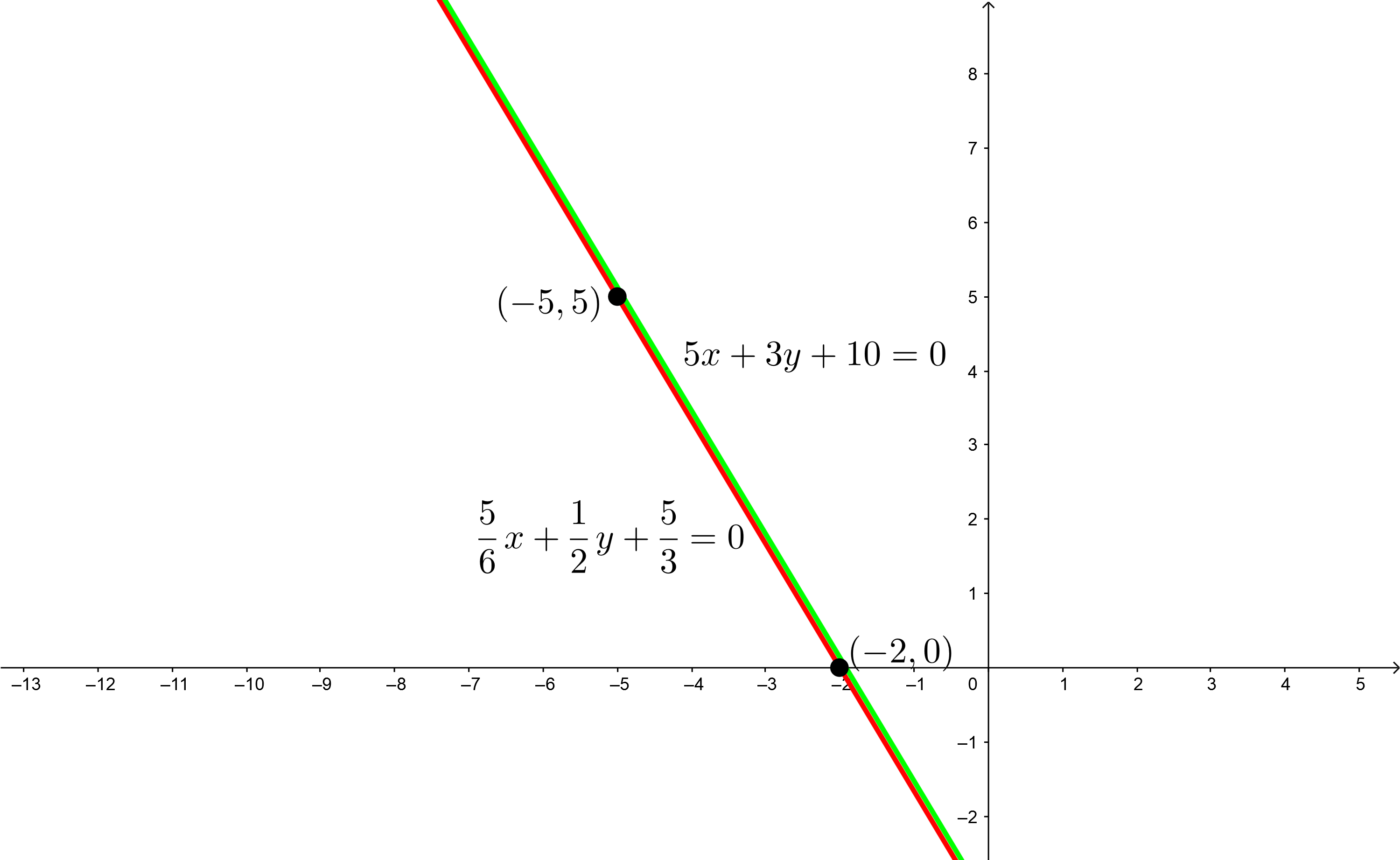
3Es gibt unendlich viele Lösungen, da die beiden Geraden gleich sind und sich in allen Punkten schneiden.
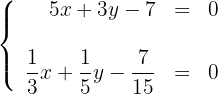
Um eine Gerade grafisch darzustellen, genügt es, zwei Punkte zu kennen und die Gerade zu zeichnen, die sie enthält.
1Wir erhalten zwei Punkte für jede der Geraden. Wir können die Schnittpunkte mit den Achsen finden oder  beliebige Werte zuweisen, um Werte für
beliebige Werte zuweisen, um Werte für  zu erhalten. Hier nehmen wir die Werte
zu erhalten. Hier nehmen wir die Werte 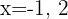 für die erste Gleichung
für die erste Gleichung
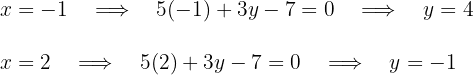 Für die erste Gleichung lauten die Punkte
Für die erste Gleichung lauten die Punkte 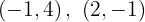 Für die zweite Gleichung, wenn wir die Werte
Für die zweite Gleichung, wenn wir die Werte 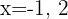 nehmen, lauten die Punkte
nehmen, lauten die Punkte 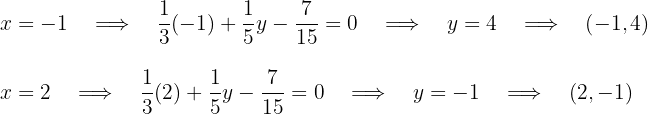
2Wir stellen die Punkte der Geraden in der kartesischen Ebene dar, zeichnen mit Hilfe eines Lineals die beiden Geraden ein und lokalisieren den Schnittpunkt der beiden Geraden
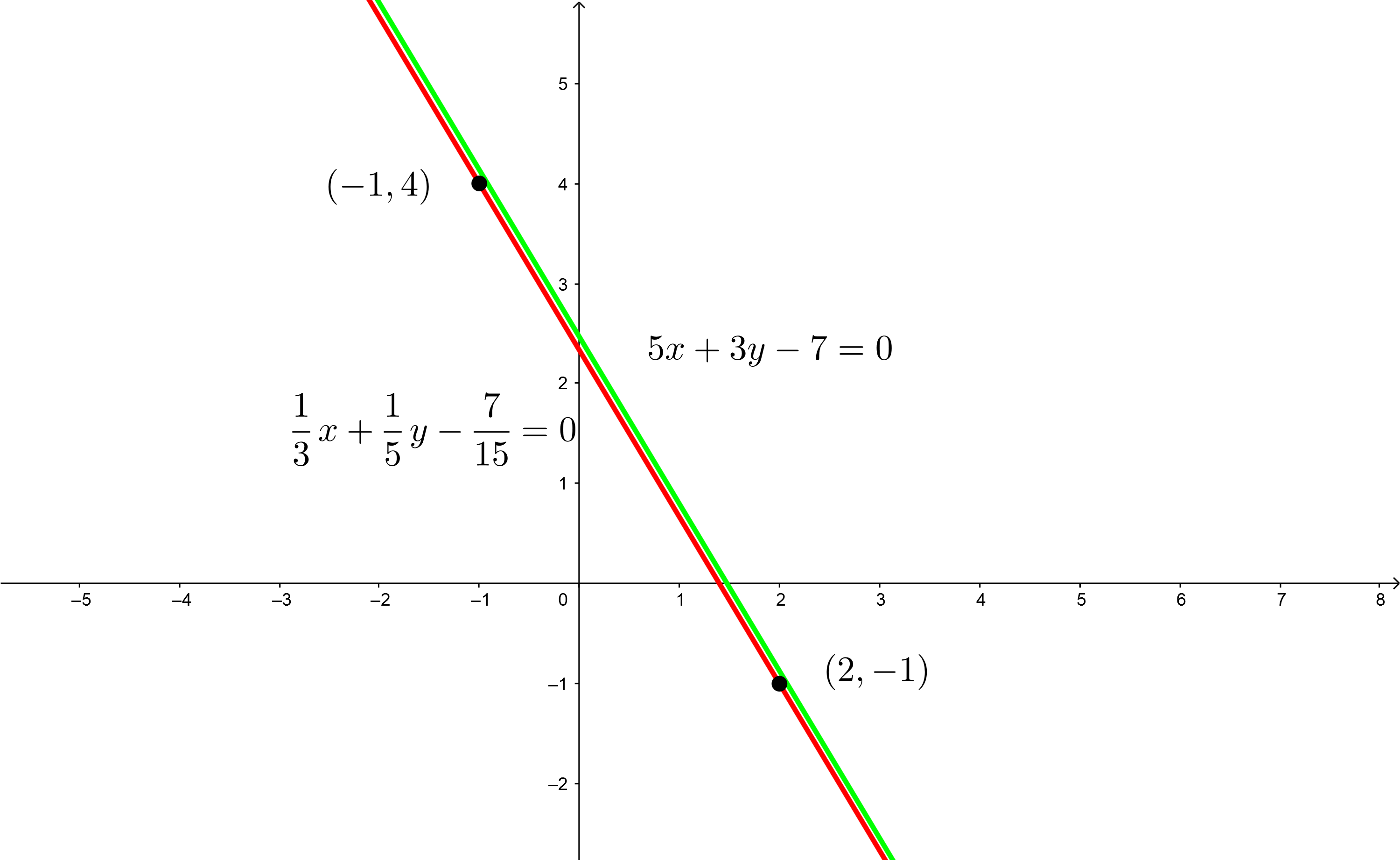
3Es gibt unendlich viele Lösungen, da die beiden Geraden gleich sind und sich in allen Punkten schneiden.
Mit KI zusammenfassen:












