Löse die folgenden Aufgaben:
Die Gleichung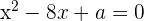 
hat zwei Lösungen und eine davon ist 
. Berechne den Parameter 
.
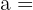
Dieses Feld ist erforderlich.
Wir wissen, dass eine Lösung der Gleichung 
ist. Wenn wir dies in die aufgestellte Gleichung einsetzen, erhalten wir Folgendes:
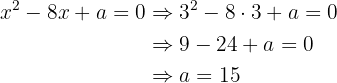
Die Gleichung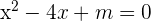 
hat zwei Lösungen und eine davon ist 
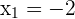. Ermittle die andere Lösung, ohne den Parameter 
zu berechnen.
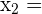
Dieses Feld ist erforderlich.
Wir bezeichnen die andere Lösung 
:
Die Summe 
der Lösungen der quadratischen Gleichung ist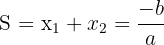 
, weshalb gilt:
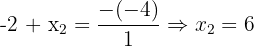
3 Gegeben ist die Gleichung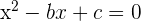 
. Berechne die Werte der Koeffizienten 
und 
, wenn du weisst, dass die Lösungen 
und 
sind.
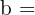
Dieses Feld ist erforderlich.
Dieses Feld ist erforderlich.
Aus der Eigenschaft der Summe ergibt sich
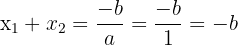
Wir wissen, dass und . Somit
Aus der Eigenschaft des Produkts ergibt sich
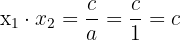
also
4 Berechne die Nullstellen der Gleichung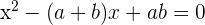 
.
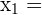
Dieses Feld ist erforderlich.
Dieses Feld ist erforderlich.
Wir berechnen die Lösungen anhand der Formel:
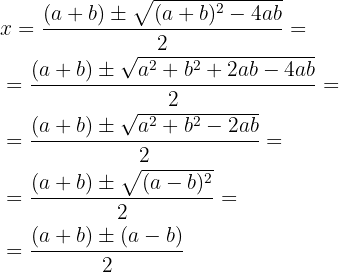
Somit lautet die Lösung
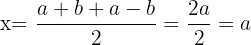
Und die andere
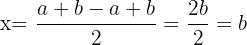
5 Berechne die Koeffizienten der quadratischen Gleichung, deren Nullstellen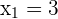 
und 
sind.
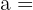
Dieses Feld ist erforderlich.
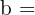
Dieses Feld ist erforderlich.
Dieses Feld ist erforderlich.
Wenn wir die Nullstellen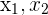 
einer quadratischen Gleichung kennen, können wir sie wie folgt schreiben
,
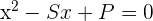wobei
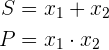
In diesem Fall haben wir 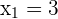und , also
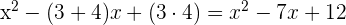
6 Finde die quadratische Gleichung, deren Lösungen die Summe 
und deren Produkt 
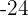ergeben.
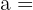
Dieses Feld ist erforderlich.
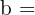
Dieses Feld ist erforderlich.
Dieses Feld ist erforderlich.
Wenn wir die Ergebnisse aus Aufgabe 4 anwenden, erhalten wir direkt die Gleichung
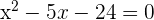
7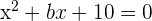 
ist eine quadratische Gleichung mit der Lösung 
. Berechne den Wert von .
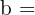
Dieses Feld ist erforderlich.
Wir wissen, dass eine Lösung der Gleichung 
ist. Wenn wir dies in die aufgestellte Gleichung einsetzen, erhalten wir:
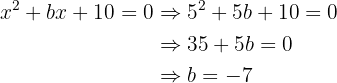
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
