Berechne die Nullstellen der folgenden Gleichungen höheren Grades als zwei und schreibe sie in aufsteigender Reihenfolge auf. Wenn eine Lösung ein Bruch ist, schreibe das Ergebnis in der Form a/b.
1

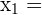
Dieses Feld ist erforderlich.
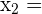
Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an

Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
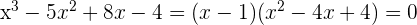
2 Da 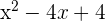 ein quadratisches Trinom ist, wird es wie folgt faktorisiert
ein quadratisches Trinom ist, wird es wie folgt faktorisiert
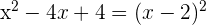
Somit ist  eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
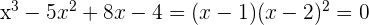
3 Die Nullstellen der Gleichung sind 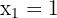 und
und 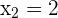
2

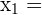
Dieses Feld ist erforderlich.
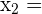
Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an
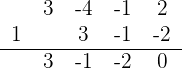
Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
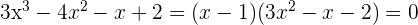
2 Wir wenden die allgemeine Formel für quadratische Gleichungen an
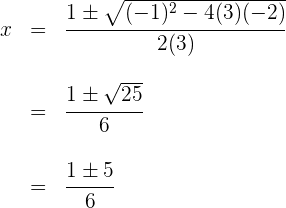
Wir berechnen die Nullstellen
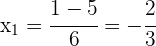
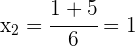
3 Die Nullstellen der Gleichung sind  und
und 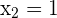 ist eine doppelte Nullstelle.
ist eine doppelte Nullstelle.
3
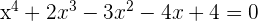
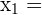
Dieses Feld ist erforderlich.
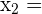
Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an

Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
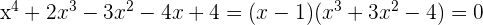
2 Wir wenden erneut die Ruffini-Regel für  an
an
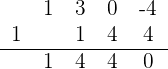
Da der Rest 0 ist, ist  eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden

3 Da  ein quadratisches Trinom ist, wird es wie folgt faktorisiert
ein quadratisches Trinom ist, wird es wie folgt faktorisiert

Somit ist  eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden

4 Die Nullstellen der Gleichung sind 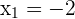 und
und 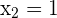
4

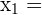
Dieses Feld ist erforderlich.
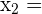
Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an
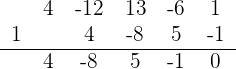
Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
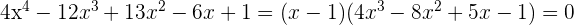
2 Wir wenden erneut die Ruffini-Regel für  an
an
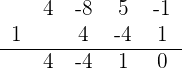
Da der Rest 0 ist, ist  eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
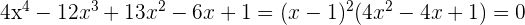
3 Da  ein quadratisches Trinom ist, kann es wie folgt faktorisiert werden
ein quadratisches Trinom ist, kann es wie folgt faktorisiert werden
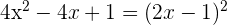
Somit ist  eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine doppelte Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
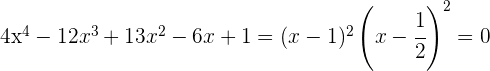
4 Die Nullstellen der Gleichung sind 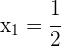 und
und 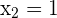
5
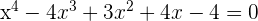
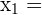
Dieses Feld ist erforderlich.
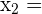
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an
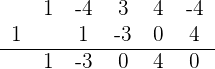
Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden

2 Wir wenden erneut die Ruffini-Regel für  an
an
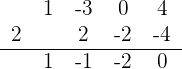
Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden

3 Wir wenden die allgemeine Formel für quadratische Gleichungen an

Wir berechnen die Nullstellen
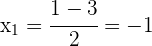
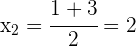
4 Die Nullstellen der Gleichung sind  und
und 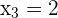
6
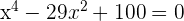
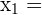
Dieses Feld ist erforderlich.
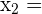
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
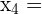
Dieses Feld ist erforderlich.
1 Wir wenden die Ruffini-Regel für  an
an
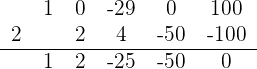
Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
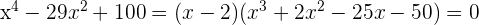
2 Wir wenden erneut die Ruffini-Regel für  an
an

Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
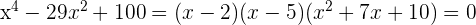
3 Wir wenden die allgemeine Formel für quadratische Gleichungen an
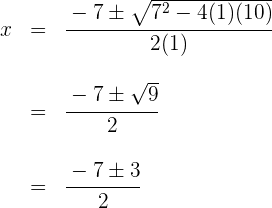
Wir berechnen die Nullstellen

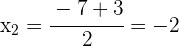
4 Die Nullstellen der Gleichung sind 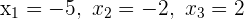 und
und 
7
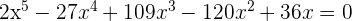
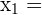
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
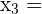
Dieses Feld ist erforderlich.
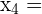
Dieses Feld ist erforderlich.
1Wir klammern den gemeinsamen Faktor aus:
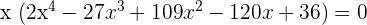
Also ist  eine Nullstelle der Gleichung.
eine Nullstelle der Gleichung.
2 Wir wenden die Ruffini-Regel für  an
an

Da der Rest 0 ist, ist  eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und sie kann wie folgt faktorisiert werden

3 Wir wenden erneut die Ruffini-Regel für 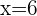 an
an

Da der Rest 0 ist, ist 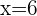 eine Nullstelle der Gleichung und kann wie folgt faktorisiert werden
eine Nullstelle der Gleichung und kann wie folgt faktorisiert werden
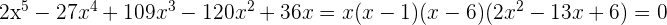
4 Wir wenden die allgemeine Formel für quadratische Gleichungen an
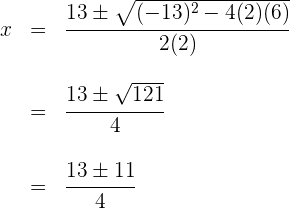
Wir berechnen die Nullstellen
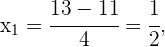

5 Die Nullstellen der Gleichung sind 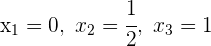 und
und 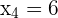
Mit KI zusammenfassen:


