Wähle die richtige Option:
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Nullstellen sind
Die Gleichung hat zwei einfache Lösungen: 
und 
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Gleichung hat eine doppelte Lösung: 
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Gleichung hat eine doppelte Lösung: 
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Gleichung hat keine reelle Lösung, da der Radikand negativ ist.
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Nullstellen sind
Die Gleichung hat zwei einfache Lösungen: 
und 
.
Die Gleichung 
hat...
Bitte wähle eine Antwort aus.
Wir lösen die Gleichung mithilfe der Formel zur Berechnung der Nullstellen einer quadratischen Gleichung
Die Gleichung hat keine reellen Lösungen, da der Radikand negativ ist.
Löse die folgenden Aufgaben:
Berechne den Wert von 
so, dass die Gleichung 
eine einzige Lösung hat.
; 
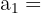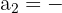
Dieses Feld ist erforderlich.
Damit die Gleichung eine doppelte Nullstelle hat, müssen wir überprüfen, ob ihre Diskriminante 0 ist.
Die Diskriminante ist 
Wir setzen die Diskriminante gleich 0 und bestimmen
Wenn also , gibt es eine doppelte Nullstelle.
2
Wir wissen, dass für 
das Polynom 
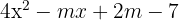eine doppelte Nullstelle hat. Berechne einen weiteren Wert für 
, sodass das besagte Polynom eine doppelte Nullstelle hat.
m =
Dieses Feld ist erforderlich.
Dass das Polynom el polinomio 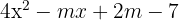eine doppelte Nullstelle hat, bedeutet, dass die Gleichung 
eine einzige Lösung hat.
Damit die Gleichung eine einzige Lösung hat, muss überprüft werden, ob die Diskriminante gleich 0 ist.
Wir berechnen und erhalten die quadratische Gleichung 
Wir lösen die Gleichung mithilfe der Formel zur Ermittlung der Nullstellen der quadratischen Gleichung
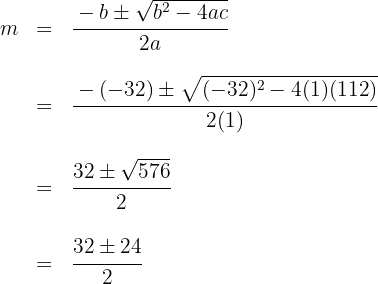
Die Nullstellen sind
Damit das gegebene Polynom also eine doppelte Nullstelle hat, muss gleich oder 
sein
Berechne für den Wert und den Wert, den du im vorherigen Abschnitt erhalten hast, die Lösung der Gleichung
/
Dieses Feld ist erforderlich.
Für wird die Gleichung zu: 
/
Dieses Feld ist erforderlich.
Für wird die Gleichung zu: 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
