Löse die folgenden Aufgaben:
1
Der Umfang eines rechteckigen Grundstücks beträgt 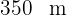 . Wie groß ist das Grundstück, wenn man weiß, dass seine Länge dreimal so groß wie seine Breite ist?
. Wie groß ist das Grundstück, wenn man weiß, dass seine Länge dreimal so groß wie seine Breite ist?
Länge  .
.
Breite  .
.
Dieses Feld ist erforderlich.
Wie groß ist die Fläche des Grundstücks? Runde auf zwei Dezimalstellen.

Dieses Feld ist erforderlich.
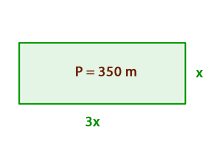
Wenn die Breite  ist, ist die Länge
ist, ist die Länge  .
.
Da der Umfang  ist, erhalten wir:
ist, erhalten wir:

Die Breite misst 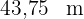 .
.
Die Länge misst 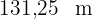 .
.
Wir berechnen die Fläche
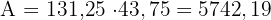
Die Fläche (auf zwei Dezimalstellen gerundet) beträgt 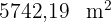
2
Wenn die Seitenlänge eines Quadrats um  zunimmt, beträgt der Umfang
zunimmt, beträgt der Umfang 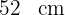 . Wie groß ist die ursprüngliche Seite des Quadrats?
. Wie groß ist die ursprüngliche Seite des Quadrats?

Dieses Feld ist erforderlich.
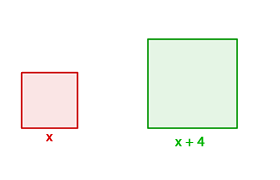
Angenommen, die Seite des ersten Quadrats ist  . Dann ist die Seite des anderen Quadrats
. Dann ist die Seite des anderen Quadrats  .
.
Da der Umfang 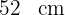 beträgt, erhalten wir
beträgt, erhalten wir
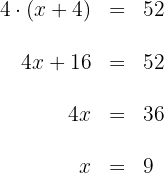
Die Seitenlänge des ursprünglichen Quadrats beträgt 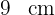 .
.
3
Berechne den Wert der Innenwinkel eines Dreiecks, wenn  um
um  größer ist als
größer ist als  und
und  um
um  größer ist als
größer ist als  .
.

 .
.
Dieses Feld ist erforderlich.

 .
.
Dieses Feld ist erforderlich.

 .
.
Dieses Feld ist erforderlich.
Wenn  der Innenwinkel im Eckpunkt
der Innenwinkel im Eckpunkt  ist, ist der Winkel im Eckpunkt
ist, ist der Winkel im Eckpunkt  gleich
gleich 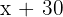 und der Winkel im Eckpunkt
und der Winkel im Eckpunkt  ist
ist 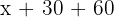 .
.
Da die Summe der Innenwinkel eines Dreiecks  beträgt, gilt:
beträgt, gilt:
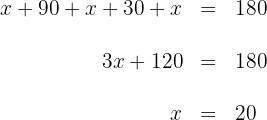
Der Winkel im Eckpunkt  misst
misst 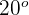 .
.
Der Winkel im Eckpunkt  misst
misst 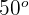
Der Winkel im Eckpunkt  misst
misst 
4
Wenn die Seitenlänge eines Quadrats um  abnimmt, beträgt der Umfang
abnimmt, beträgt der Umfang 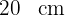 . Wie lange ist die Seitenlänge des ursprünglichen Quadrats?
. Wie lange ist die Seitenlänge des ursprünglichen Quadrats?

Dieses Feld ist erforderlich.
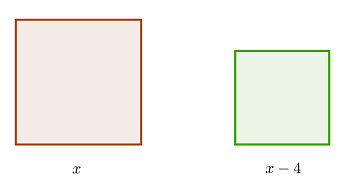
Angenommen, die Seite des ersten Quadrats ist  . Dann ist die Seite des anderen Quadrats
. Dann ist die Seite des anderen Quadrats  .
.
Da der Umfang des 2. Quadrats 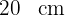 beträgt, gilt:
beträgt, gilt:
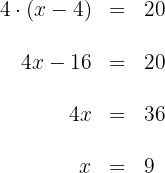
Die Seitenlänge des ursprünglichen Quadrats misst 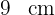 .
.
5
Berechne den Wert der Innenwinkel eines Dreiecks, wenn  doppelt so groß wie
doppelt so groß wie  ist und
ist und  gleich der Summe von
gleich der Summe von  und
und  ist.
ist.

 .
.
Dieses Feld ist erforderlich.

 .
.
Dieses Feld ist erforderlich.

 .
.
Dieses Feld ist erforderlich.
Wenn  der Winkel
der Winkel  ist, ist der Winkel
ist, ist der Winkel  gleich
gleich  und der Winkel
und der Winkel  gleich
gleich 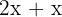 .
.
Da die Summe der Innenwinkel eines Dreiecks gleich  ist, ergibt sich Folgendes:
ist, ergibt sich Folgendes:

Der Winkel im Eckpunkt  misst
misst  .
.
Der Winkel im Eckpunkt  misst
misst 
Der Winkel im Eckpunkt  misst
misst 
6
Wenn die Höhe eines gleichschenkligen Dreiecks  der Grundseite entspricht und der Flächeninhalt
der Grundseite entspricht und der Flächeninhalt 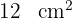 beträgt, wie groß ist dann der Umfang des Dreiecks?
beträgt, wie groß ist dann der Umfang des Dreiecks?

Dieses Feld ist erforderlich.
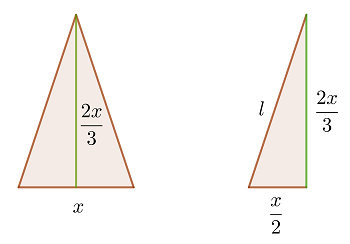
 ist die Grundseite. Somit ist die Höhe
ist die Grundseite. Somit ist die Höhe  .
.
Da die Fläche 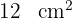 beträgt, gilt:
beträgt, gilt:
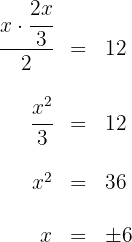
Die Grundseite des Dreiecks misst  und seine Höhe
und seine Höhe  .
.
Die Höhe teilt das gleichschenklige Dreieck in zwei gleiche rechtwinklige Dreiecke. Wir wenden den Satz des Pythagoras an, um die beiden verbleibenden  Seiten zu finden.
Seiten zu finden.
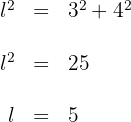
Der Umfang ist 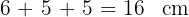 .
.
7
Berechne den Radius und die Fläche eines Kreises, dessen Umfang 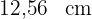 ist. Verwende
ist. Verwende 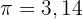 .
.
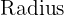
 .
.
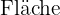
 .
.
Dieses Feld ist erforderlich.
Wenn  der Radius und
der Radius und 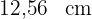 der Umfang ist, gilt:
der Umfang ist, gilt:
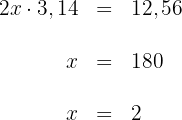
Der Flächeninhalt des Kreises beträgt 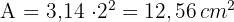 .
.
8
Wenn der Radius eines Kreises um 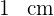 zunimmt, beträgt sein Umfang
zunimmt, beträgt sein Umfang 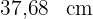 . Wie groß ist der Umfang des ursprünglichen Kreises? Verwende
. Wie groß ist der Umfang des ursprünglichen Kreises? Verwende 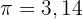 .
.

Dieses Feld ist erforderlich.
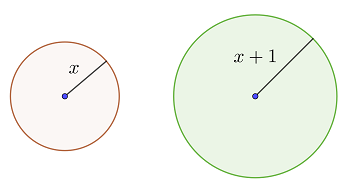
Der Radius ist  . Somit hat der 2. Kreis den Radius
. Somit hat der 2. Kreis den Radius  .
.
Da der Umfang des 2. Kreises 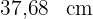 beträgt, gilt:
beträgt, gilt:
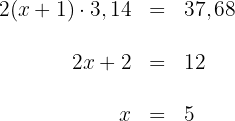
Der Umfang der ursprünglichen Kreises beträgt
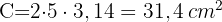 .
.
9
Wenn die Seitenlänge eines Würfels um  zunimmt, beträgt sein Volumen
zunimmt, beträgt sein Volumen  . Wie groß ist das Volumen des ursprünglichen Würfels?
. Wie groß ist das Volumen des ursprünglichen Würfels?

Dieses Feld ist erforderlich.
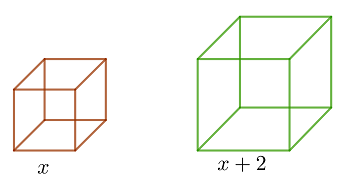
Angenommen, die Seite des ersten Würfels ist  . Dann ist die Seite des zweiten Würfels
. Dann ist die Seite des zweiten Würfels  .
.
Da der zweite Würfel das Volumen  hat, folgt daraus, dass
hat, folgt daraus, dass

Das Volumen des ursprünglichen Würfels beträgt
 .
.
10
Wenn die Höhe eines geraden Kreiszylinders mit dem Radius  um
um  abnimmt, beträgt sein Volumen
abnimmt, beträgt sein Volumen 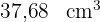 . Wie lautet das Volumen des ursprünglichen Zylinders? Verwende
. Wie lautet das Volumen des ursprünglichen Zylinders? Verwende 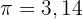

Dieses Feld ist erforderlich.
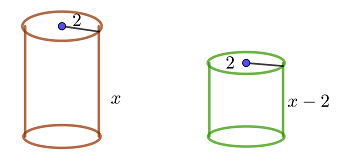
Die Höhe des 1. Zylinders ist  . Somit beträgt die Höhe des 2. Zylinders
. Somit beträgt die Höhe des 2. Zylinders  .
.
Da der 2. Zylinder ein Volumen von 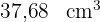 hat, gilt:
hat, gilt:
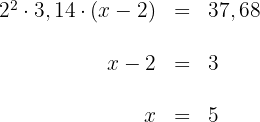
Das Volumen des ursprünglichen Zylinders beträgt
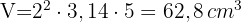 .
.
Mit KI zusammenfassen:


