Ein Vater ist 35 Jahre alt, sein Sohn 5 Jahre. In wievielen Jahren wird der Vater dreimal so alt sein wie sein Sohn?
1 Alter des Sohnes in 
Jahren : 
2 Alter des Vaters in Jahren: 
2 In Jahren soll das Alter des Vaters soll dreimal so hoch sein wie das Alter des Sohnes:
4 Löse die Klammer auf
5 Gruppiere die Terme und löse nach x auf, indem du beide Seiten durch 2 teilst:
6 Die Antwort ist: nach 10 Jahren.
Das Doppelte einer Zahl minus ihrer Hälfte ergibt 54. Welche Zahl suchen wir?
1 Zahl:
2 Das Doppelte der Zahl: 
3 Die Hälfte der Zahl: 
4 Das Doppelte minus die Hälfte ergibt 54:
5 Gruppiere die Terme und löse nach x auf
6 Die gesuchte Zahl ist: 36
Die Grundseite eines Rechtecks ist doppelt so lang wie seine Höhe. Wie lang sind Grundseite und Höhe, wenn der Umfang des Rechtecks 30 cm beträgt?
1 Höhe:
2 Grundseite:
3 Der Umfang des Rechtecks ist gleich die Summe der doppelten Höhe plus doppelter Grundseite :
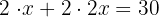
4 Summiere und löse auf
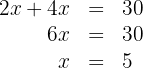
5 Die gesuchte Höhe ist: 5 cm
Die gesuchte Grundseite ist 10 cm lang
An einem Treffen nehmen doppelt soviele Frauen wie Männer teil und dreimal soviele Kinder wie Männer und Frauen zusammen. Wieviele Männer, Frauen und Kinder treffen sich, wenn es sich insgesamt um 96 Personen handelt?
1 Männer
2 Frauen
3 Kinder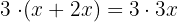 
4 Insgesamt 96 Personen:
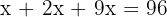
5 Summiere und löse auf
6 Männer: 8
Frauen: 16
Kinder: 72
7/8 eines Öltanks wurden bereits verbraucht. Wenn wir 38 l hineinfüllen, ist der Tank zu 3/5 voll. Wieviele Liter Öl passen insgesamt in den Tank?
1 Mit bezeichnen wir das aktuelle Fassungsvermögen des Tanks. Da 7/8 seines Inhalts verbraucht wurden, ist die Gleichung:
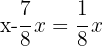
2 Wenn wir 38 l nachfüllen, ist der Tank zu 3/5 voll:
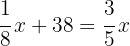
3 Entferne die Nenner mithilfe des kgV: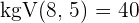 
4 Gruppiere die Terme und löse auf
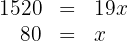
5 Das Fassungsvermögen des Tanks beträgt: 80 l
Auf einem Bauernhof werden Schweine und Truthähne gehalten. Insgesamt kann man dort 35 Köpfe und 116 Beine zählen. Wieviele Schweine und Truthähne leben auf dem Hof?
1 Schweine
2 Truthähne 
3 Die Gesamtzahl der Beine ergibt sich aus dem vierfachen der Zahl der Schweine plus dem Zweifachen der Zahl der Truthähne.
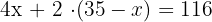
4 Löse die Klammer auf
5 Gruppiere die Terme und löse auf
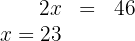
6 Schweine: 23
Truthähne: 35 - 23 = 12
Luis ist mit dem Auto verreist und hat auf dem Weg 20 l Benzin verbraucht. Er ist die Strecke in zwei Etappen gefahren: für die erste Etappe hat er 2/3 des Benzins im Tank verbraucht; für die zweite die Hälfte des Benzins, die nach der ersten noch im Tank war. Wieviele Liter Benzin hatte er insgesamt beim Start im Tank und wieviele hat er bei den einzelnen Etappen verbraucht?
1 Liter Benzin, die er beim Start im Tank hatte:
Erste Etappe 
Zweite Etappe 
2 In beiden Etappen hat er insgesamt 20 l verbraucht:
3 Entferne die Nenner, summiere und löse auf:
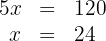
4 Die gesuchten Lösungen sind:
Benzin im Tank beim Start: 24 l
Benzinverbrauch erste Etappe: 16 l
Benzinverbrauch zweite Etappe: 4 l
Anna kauft mit einem Drittel ihres Geldes ein Buch und mit zwei Dritteln des übrigen Geldes einen Comic. Nach dem Einkauf hat sie noch 12 € übrig. Wieviel Geld hatte Anna insgesamt?
1 Geld Gesamt
Buch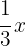 
Comic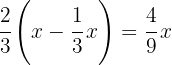 
2 Anna hatte insgesamt das Geld, das das Buch kostete, plus das Geld, das der Comic kostete, plus das Geld, das am Ende noch übrig ist:
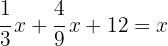
3 Entferne die Nenner
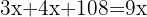
4 Gruppiere die Terme und löse auf
5 Anna hatte insgesamt 24 €
Eine Zahl besteht aus zwei konsekutiven Ziffern. Die größere Ziffer steht an der Zehner-Stelle, die kleinere an der Einer-Stelle. Die Zahl ist gleich sechsmal so hoch wie die Summe ihrer Ziffern. Welche Zahl ist gesucht?
1 Einer-Ziffer
Zehner-Ziffer 
2 Wenn wir eine Zahl mit zwei Ziffern haben, z.B. die Zahl 65, können wir sie auf diese Weise zerlegen: 6 · 10 + 5.
3 Unsere Zahl aus zwei Ziffern ist also: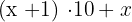 
4 Da die Zahl sechsmal so hoch wie die Summe der beiden Ziffern ist, gilt: 
. Wir erhalten also:
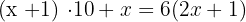
5 Löse die Klammer auf und berechne:
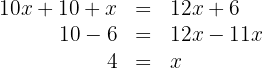
6 Die Ergebnisse sind
Einer-Ziffer: 4
Zehner-Ziffer: 5
Die gesuchte Zahl ist: 54
3/4 des Alters des Vaters von Jan entsprechen 15 Jahren mehr als Jan´s Alter. Vor vier Jahren war der Vater doppelt so alt wie Jan. Wie alt sind beide?
1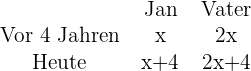 
2 Formuliere die Gleichung der Aufgabe:
3 Löse die Klammern auf, gruppiere die Terme und löse auf
4 Das Alter von Jan ist: 32 + 4 = 36. Das Alter seines Vaters ist: 2 · 32 + 4 = 68
Zwei Bauarbeiter erledigen eine Aufgabe zusammen innerhalb von 14 Stunden. Wie lange brauchen sie allein, wenn einer der beiden doppelt so schnell arbeitet wie der andere?
1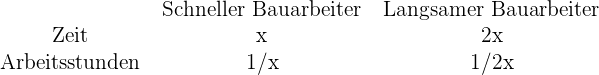 
2 Formuliere die Gleichung der Aufgabe:
3 Ermittle das kgV, um die Nenner entfernen zu können:
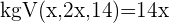
4 Multipliziere beide Seiten und löse auf
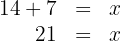
5 Die Lösungen sind:
Schneller Bauarbeiter: 21 Stunden
Langsamer Bauarbeiter: 42 Stunden
Ermittle die Größe der drei Innenwinkel eines Dreiecks mit folgenden Bedingungen: B ist 40° größer als C; A ist 40° größer als B.
1 C:
B: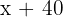 
A: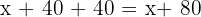 
2 Die Summe der Innenwinkel eines Dreiecks beträgt 180º
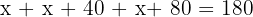
3 Gruppiere die Terme
4 Summiere und löse auf
5 Die Winkel betragen:
C = 20º, B = 20º + 40º = 60º, A = 60º + 40º = 100º
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
