Übungsaufgaben zu linearen Gleichungen

Eliminiere die Unbekannte, indem du auf beiden Seiten durch  teilst. Du kannst auch sagen, dass die , die im ersten Glied multipliziert wurde, im zweiten Glied dividiert wird.

Wenn du die gleichen Terme zusammenfasst, musst du die beiden Glieder und , addieren, damit man eine äquivalente Gleichung erhält.

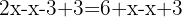
In der Praxis wird oft gesagt, dass ein Term, der in einem Glied addiert wird, durch Subtraktion von  in das andere Glied übergeht, und wenn übrig bleibt, durch Addition von in das andere Glied übergeht. Addiere:

Verwende die Distributiv-Eigenschaft, um die Klammer aufzulösen, d. h. du multiplizierts jeden algebraischen Term, der sich innerhalb der Klammer befindet, mit so dass auf der linken Seite folgendes steht:

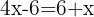
Gruppiere gleichartige Terme, das addierte x wandert durch Subtraktion auf die andere Seite und die verbelibende wird addiert. Addiere also:

Eliminiere die Unbekannte, die wandert durch Division auf die andere Seite

Um die Nenner zu entfernen, musst du das kleinste gemeinsame Vielfache von und finden

Multipliziere beide Teile der Gleichung mit dem Mittelwert, in diesem Fall , und erhältst:

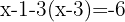
Multipliziere unter Verwendung der Distributiv-Eigenschaft, löse die Klammer auf, gruppiere und addiere gleiche Terme:

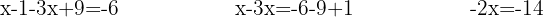
Löse die Unbekannte:

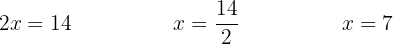
Multipliziere mit jedem Term innerhalb der Klammer (distributive Eigenschaft), um die Klammer aufzulösen und zu vereinfachen:

Gruppiere und addiere gleiche Terme:

Unter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern multipliziert man die erste Klammer mit und die zweite mit .

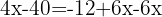
Fasse gleiche Terme zusammen

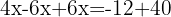
Addiere die gleichen Terme und löst nach x auf

Löse mit Hilfe der Distributiv-Eigenschaft die Klammer auf, indem du die erste Klammer mit und die zweite Klammer mit multiplizierst.

Fasse gleiche Terme zusammen

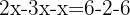
Addiere die gleichen Terme und löst nach x auf

Um die Nenner zu eliminieren, musst du das kleinste gemeinsame Vielfache von , y

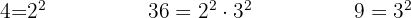
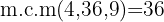
Teile den gemeinsamen Nenner durch jeden Nenner und multipliziere das Ergebnis mit dem entsprechenden Zähler

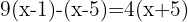
Multipliziere mit der Distributiv-Eigenschaft der Klammern die erste mit , die zweite mit und die dritte mit .

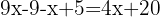
Gruppiere gleiche Terme zusammen

Addiere die gleichen Terme und löst nach x auf

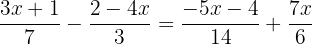
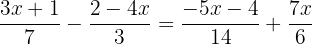Um die Nenner zu entfernen, musst du das kleinste gemeinsame Vielfache von ,, und finden.

Teile den gemeinsamen Nenner durch jeden Nenner und multiplizierst das Ergebnis mit dem entsprechenden Zähler

Multipliziere unter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern die erste Klammer mit , die zweite mit 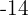, und die dritte Klammer mit .

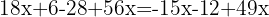
Fasse gleiche Terme zusammen

Addiere die gleichen Terme und löse nach x auf

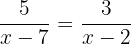
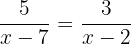Damit die Gleichheit der beiden Brüche erfüllt ist, muss das Produkt der Zwecke gleich dem Produkt der Mittel sein.

Als Alternative kannst du auch das kleinste gemeinsame Vielfache finden, das ist, weil die beiden Binome nicht kürzbar sind. Dann teilst du den Mittelwert durch jeden Nenner und das Ergebnis wird mit dem entsprechenden Zähler multipliziert.

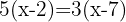
Unter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern multiplizierst du die erste Klammer mit und die zweite mit .

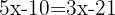
Addiere die gleichen Terme

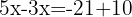
Löse die Unbekannte:

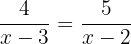
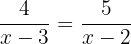Damit die Gleichheit der beiden Brüche erfüllt ist, muss der Extremwert dem Mitelwert entsprechen.

Als Alternative kannst du auch das kleinste gemeinsame Vielfache finden, das 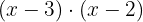ist, weil die beiden Binome nicht kürzbar sind. Dann teilst du den Mittelwert durch jeden Nenner und das Ergebnis wird mit dem entsprechenden Zähler multipliziert.

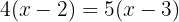
Multipliziere unter nter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern die erste Klammer mit und die zweite mit .

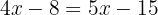
Gruppiere gleiche Terme zusammen

Löse die Unbekannte:

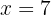
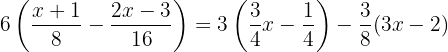
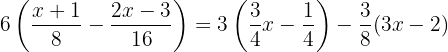Unter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern multipliziert man die erste Klammer mit , die zweite mit und die dritte mit .

Gut zu wissen: Wenn eine ganze Zahl mit einem Bruch multipliziert wird, löst du diesen, indem die ganze Zahl mit dem Zähler des Bruchs multipliziert wird und der Nenner derselbe bleibt.

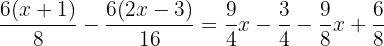
Verwende die distributive Eigenschaft, um oben im Bruch die Klammern aufzulösen

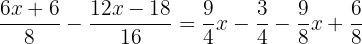
Um die Nenner zu entfernen, musst du das kleinste gemeinsame Vielfache von , und finden.

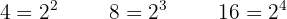
Dividiere den gemeinsamen Nenner durch jeden Nenner und multiplizierst das Ergebnis mit dem entsprechenden Zähler.

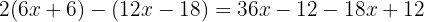
Verwende die Distributiv-Eigenschaft, um die Klammern aufzulösen, multiplizierst die erste Klammer mit und vereinfachst unter Beachtung des Vorzeichenwechsels.

Fasse gleiche Terme zusammen

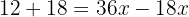
Löse die Unbekannte:

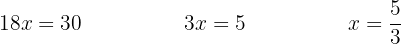
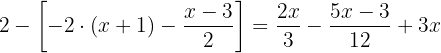
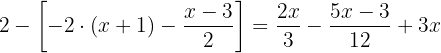In diesem Fall ist es zweckmäßig, zunächst den Term 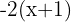aufzulösen. Beim Auflösen kannst du die eckige Klammer durch eine normale Klammer ersetzen.

Multipliziere die Terme innerhalb der Klammern mit -1, so dass du das negative Vorzeichen und die Klammern aus der Gleichung entfernen kannst:

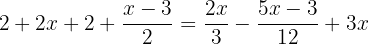
Um die Nenner zu entfernen, musst du das kleinste gemeinsame Vielfache von 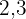und finden.

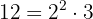
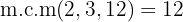
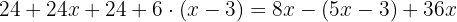
Multipliziere nter Verwendung der Distributiv-Eigenschaft zur Auflösung der Klammern die erste Klammer mit und die zweite mit auf:

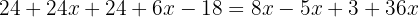
Gruppiere gleiche Terme zusammen:

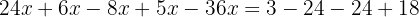
Addieret:

Teile die beiden Mitglieder durch

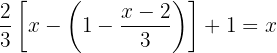
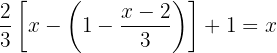Multipliziere die Terme innerhalb der Klammer durch , so dass du das negative Vorzeichen und die Klammer aus der Gleichung entfernen und die eckige durch eine runde Klammer ersetzen kannst.

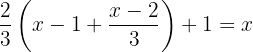
Verwende die Distributiv-Eigenschaft, um die Klammern aufzulösen.

Gut zu wissen: Wenn du einen Bruch mit einem anderen multiplizierst, musst du den Zähler mit dem Zähler und den Nenner mit dem Nenner multiplizieren.

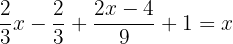
Um die Nenner zu entfernen, muss man das kleinste gemeinsame Vielfache von und finden.

Fasse gleiche Terme zusammen:

Addiere und löse nach x auf: