Kapitel
- Finde die quadratische Gleichung
- Faktorisierung
- Finde den Wert k
- Finde die gesuchten Werte
- Übung zur Altersberechnung
- Berechnung eines Grundstücks
- Proportionale Dreiecke
- Berechne die Fläche des Gartens
- Ähnlichkeitskriterium in Rechtecken
- Berechne die gesuchte Zahl
- Strukturiere die quadratische Gleichung und berechne
- Füllzeit eines Pools berechnen
- Finde die vorgegebenen Werte
- Berechnung eines Volumens
- Befüllen eines Tanks
Finde die quadratische Gleichung
Schreibe eine quadratische Gleichung mit den Lösungen: 3 y −2.
1Da du die Wurzeln der Gleichung kennst, kannst du die Gleichung so darstellen:
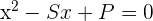
Dabei ist  die Summe der Wurzeln und
die Summe der Wurzeln und  das Produkt der Wurzeln
das Produkt der Wurzeln
2Berechne  und
und 

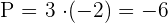
3Die gesuchte quadratische Gleichung lautet:

Faktorisierung
Faktorisieren: 
1Löse mit der abc-Formel von quadratischen Gleichungen
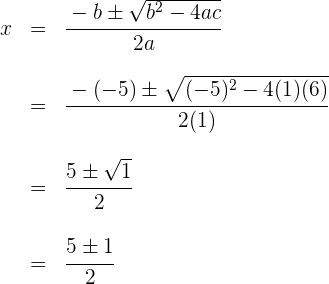
Die Wurzeln sind

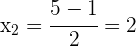
2Wenn du die Wurzeln der Gleichung kennst, kannst du sie wie folgt faktorisieren:
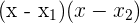
3Die gesuchte Faktorisierung ist also
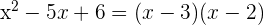
Finde den Wert k
Bestimme  so, dass in der Gleichung
so, dass in der Gleichung 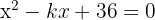 die Wurzeln gleich sind.
die Wurzeln gleich sind.
1Damit die beiden Wurzeln gleich sind, muss die Diskriminante  gleich Null sein. Berechne die Diskriminante
gleich Null sein. Berechne die Diskriminante

2Setze das Ergebnis gleich Null
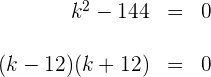
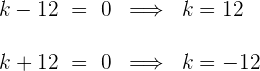
3Setze jeden Faktor auf Null und suche die Werte von  damit die Wurzeln gleich sind
damit die Wurzeln gleich sind
Finde die gesuchten Werte
Die Summe von zwei Zahlen ist 5 und ihr Produkt ist -84. Finde diese beiden Zahlen.
1Wenn du die Wurzeln der Gleichung kennen würdest, könntest du die Gleichung schreiben als:
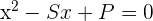
Dabei ist  die Summe der Wurzeln und
die Summe der Wurzeln und  ist das Produkt der Wurzeln
ist das Produkt der Wurzeln
2Du weißt, dass 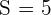 und
und 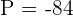 , also erhältst du:
, also erhältst du:
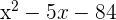
3Löse die quadratische Gleichung 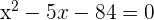
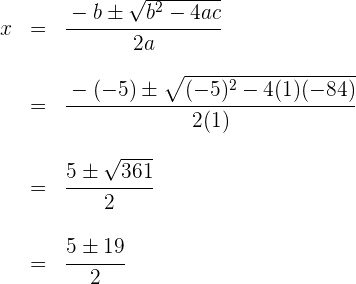
Die Wurzeln sind
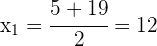
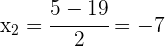
Die gesuchten Zahlen sind also  y
y 
Übung zur Altersberechnung
In 11 Jahren wird Peters Alter das halbe Quadrat des Alters sein, das er vor 13 Jahren hatte. Berechne das Alter von Peter.
1Benenne die Variablen aus der Aufgabenstellung:
Aktuelles Alter: 
Alter vor 13 Jahren: 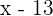
Alter in 11 Jahren: 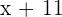
2Stelle die entsprechende Gleichung auf:
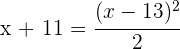
3Quadriere das Binom, entferne die Nenner und du erhältst die Gleichung:
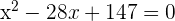
4Löse die Gleichung
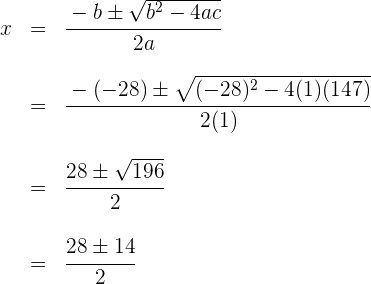
Die Wurzeln sind
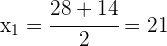

 ist keine gültige Lösung, denn wie alt wäre er dann vor 13 Jahren gewesen?
ist keine gültige Lösung, denn wie alt wäre er dann vor 13 Jahren gewesen?
Somit beträgt das aktuelle Alter  Jahre
Jahre
Berechnung eines Grundstücks
Zur Umzäunung eines rechteckigen Grundstücks von 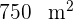 wurde ein Zaun von
wurde ein Zaun von  verwendet. Berechne die Abmessungen des Grundstücks.
verwendet. Berechne die Abmessungen des Grundstücks.
1Stelle das Grundstück dar

wobei
Semiperimeter 
Grundfläche 
Höhe 
2Die Fläche ist gleich Grundfläche mal Höhe
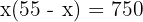
3Löse die Klammern auf und finde die Wurzeln
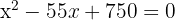
 y
y 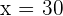
Die Abmessungen des Grundstücks sind also:
Grundfläche  und Höhe
und Höhe 
Grundfläche  und Höhe
und Höhe
Proportionale Dreiecke
Die drei Seiten eines rechtwinkligen Dreiecks sind proportional zu den Zahlen 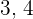 y
y  . Finde die Länge der einzelnen Seiten, wenn du weißt, dass der Flächeninhalt des Dreiecks
. Finde die Länge der einzelnen Seiten, wenn du weißt, dass der Flächeninhalt des Dreiecks 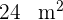 ist.
ist.
1Stelle die bereitgestellten Daten dar
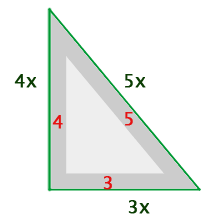
Erste Seite:  (Grundfläche)
(Grundfläche)
Zweite Seite:  (Höhe)
(Höhe)
Dritte Seite: 
2Wende die Formel für den Flächeninhalt eines Dreiecks an

3Entferne die Nenner und löse die Gleichung

 ist keine Lösung, da eine Seite keine negative Länge haben kann. Somit sind die Lösungen:
ist keine Lösung, da eine Seite keine negative Länge haben kann. Somit sind die Lösungen:
Erste Seite: 
Zweite Seite: 
Dritte Seite: 
Berechne die Fläche des Gartens
Ein rechteckiger Garten mit  Länge und
Länge und 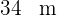 Breite wird von einem Sandweg mit gleichmäßiger Breite umgeben. Berechne die Breite dieses Sandwegs, wenn er eine Fläche von
Breite wird von einem Sandweg mit gleichmäßiger Breite umgeben. Berechne die Breite dieses Sandwegs, wenn er eine Fläche von 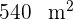 hat.
hat.
1Stelle die bereitgestellten Daten dar

 steht für die Breite der Straße
steht für die Breite der Straße
2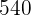 ist gleich der Gesamtfläche minus der Fläche des Gartens
ist gleich der Gesamtfläche minus der Fläche des Gartens
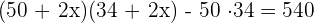
3Löse die Klammern auf, berechne und vereinfache die Gleichung, indem du auf beiden Seiten durch 4 dividierst
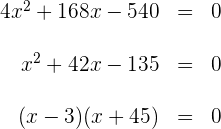
Die Breite der Straße beträgt also  .
.
 ist keine Lösung, da die Abstände positiv sein müssen.
ist keine Lösung, da die Abstände positiv sein müssen.
Ähnlichkeitskriterium in Rechtecken
Berechne die Abmessungen eines Rechtecks, dessen Diagonale  , misst, wobei du weißt, dass es einem anderen Rechteck ähnelt, dessen Seiten
, misst, wobei du weißt, dass es einem anderen Rechteck ähnelt, dessen Seiten 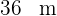 und
und  messen.
messen.
1Die Seiten haben die 12 gemeinsam, also erhältst du mit Hilfe der Ähnlichkeit:
Grundfläche 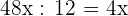
Höhe 

2Wende den Satz des Pythagoras an
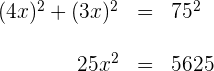
3Löse die letzte Gleichung und erhalte 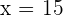 . Die Abmessungen des angeforderten Rechtecks sind also:
. Die Abmessungen des angeforderten Rechtecks sind also:
Grundfläche: 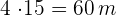
Höhe: 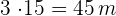
Berechne die gesuchte Zahl
Gesucht wird eine ganze Zahl, deren Summe mit dem Kehrwert  ergibt.
ergibt.
1Berücksichtige
Gesuchte Zahl: 
Kehrwert der Zahl: 
2Berechne die angegebene Summe
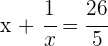
3Löse die rationale Gleichung
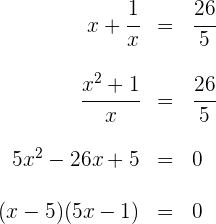
Die Lösungen der Gleichung sind  und
und 
Die gesuchte Zahl ist  , da
, da  keine Lösung ist, weil es keine ganze Zahl ist.
keine Lösung ist, weil es keine ganze Zahl ist.
Strukturiere die quadratische Gleichung und berechne
Berechne zwei natürliche Zahlen, deren Differenz zwei ist und die Summe ihrer Quadratzahlen 580 ist. Wie lauten diese Zahlen?
1Du kennst:
Erste Zahl: 
Zweite Zahl: 
Drücke die Summe der Quadratzahlen aus
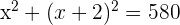
2Erhöhe das Binom zum Quadrat, berechne und vereinfache die Gleichung, indem du auf beiden Seiten durch 2 dividierst
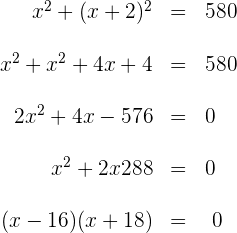
3Die Lösungen der Gleichung sind  und
und 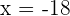
Erste Zahl: 
Zweite Zahl: 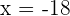
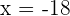 ist keine Lösung für das Problem, da es sich nicht um eine natürliche Zahl handelt
ist keine Lösung für das Problem, da es sich nicht um eine natürliche Zahl handelt
Füllzeit eines Pools berechnen
Zwei Rohre  und
und  füllen zusammen einen Pool in zwei Stunden.
füllen zusammen einen Pool in zwei Stunden.  schafft es alleine in drei Stunden weniger als
schafft es alleine in drei Stunden weniger als  . Wie viele Stunden benötigt jedes einzelne?
. Wie viele Stunden benötigt jedes einzelne?
1Du kennst:
Zeit von 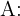

Zeit von 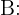

2In einer Stunde passiert folgendes:

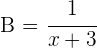
Du weißt auch, dass die 2 Rohre zusammen in einer Stunde den halben Pool füllen

3Substituiere:
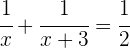
Du hast eine rationale Gleichung und musst daher zunächst die Nenner entfernen
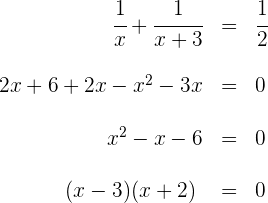
Die möglichen Lösungen sind also  und
und  , wobei letzteres keine Lösung ist, da die Zeit negativ wäre.
, wobei letzteres keine Lösung ist, da die Zeit negativ wäre.
4Prüfe, ob  eine Lösung ist:
eine Lösung ist:
Nach einer Stunde passiert folgendes:

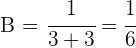
Nach 2 Stunden:
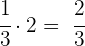

Der Pool wird folglich in 2 Stunden voll sein
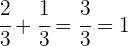
Der Pool ist nach 2 Stunden vollständig gefüllt. Die angeforderte Zeit ist also:
Zeit von 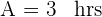
Zeit von 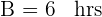
Finde die vorgegebenen Werte
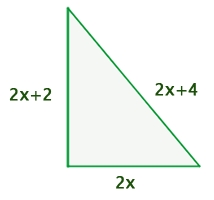
Die Seiten eines rechtwinkligen Dreiecks haben Maße in Zentimetern von drei aufeinanderfolgenden geraden Zahlen. Finde die Werte dieser Seiten.
1Stelle die bereitgestellten Daten dar

Erste Kathete: 
Zweite Kathete: 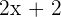
Hypotenuse: 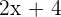
2Wende den Satz des Pythagoras an
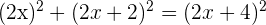
3Erhöhe das Binom zum Quadrat, berechne und vereinfache die Gleichung, indem du auf beiden Seiten durch 4 dividierst
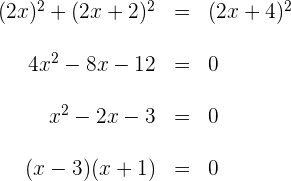
4Die Lösungen der Gleichung sind 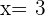 und
und 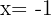 . Die gesuchten Maße entsprechen somit
. Die gesuchten Maße entsprechen somit 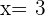
Erste Kathete: 
Zweite Kathete: 
Hypotenuse: 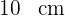
Ignoriere  , da die Abstände positiv sind
, da die Abstände positiv sind
Berechnung eines Volumens
Ein rechteckiges Papier ist  länger als es breit ist. Eine Schachtel von
länger als es breit ist. Eine Schachtel von 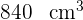 wird hergestellt, indem an jeder Ecke ein Quadrat von
wird hergestellt, indem an jeder Ecke ein Quadrat von  geschnitten und die Kanten gefaltet werden. Ermittle die Abmessungen der Schachtel.
geschnitten und die Kanten gefaltet werden. Ermittle die Abmessungen der Schachtel.
1Stelle die bereitgestellten Daten dar
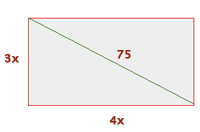
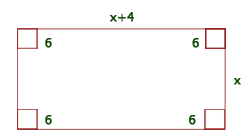
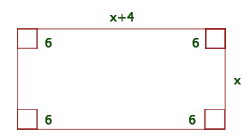
Breite: 
Länge: 
Höhe: 
2Das Volumen der Schachtel, die ein rechteckiges Prisma ist, lautet 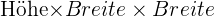
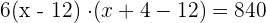 (x − 12) · (x −8) = 140
(x − 12) · (x −8) = 140
3Löse die obige Gleichung

Die Lösungen der Gleichung sind  und
und  . Die gesuchten Maße lauten also:
. Die gesuchten Maße lauten also:
Breite: 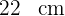
Länge: 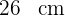
Verwerfe die Lösung  , weil eine Länge nicht negativ sein kann
, weil eine Länge nicht negativ sein kann
Befüllen eines Tanks
Ein Rohr braucht zwei Stunden länger als das andere, um einen Tank zu füllen, und wenn beide zusammen auffüllen benötigen sie 1 Stunde und 20 Minuten. Wie lange wird es dauern, bis jedes einzelne Rohr den Tank aufgefüllt hat?
1Berücksichtige
Benötigte Zeit des ersten Rohres: 
Benötigte Zeit des zweiten Rohres: 
2In einer Stunde passiert folgendes:

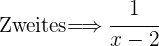
Du weißt auch, dass in einer Stunde und 20 Minuten, also in  Stunden die 2 Rohre zusammen einen Tank füllen
Stunden die 2 Rohre zusammen einen Tank füllen
3Substituiere:
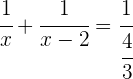
Du hast eine rationale Gleichung und musst daher zunächst die Nenner entfernen
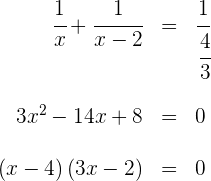
Die möglichen Lösungen sind also  und
und  , wobei letzteres keine Lösung ist, da die Zeit, die das zweite Rohr benötigt, negativ wäre.
, wobei letzteres keine Lösung ist, da die Zeit, die das zweite Rohr benötigt, negativ wäre.
4Die verwendeten Zeiten sind also:
Benötigte Zeit des ersten Rohres: 
Benötigte Zeit des zweiten Rohres: 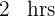
Mit KI zusammenfassen:



