Löse die folgenden nichtlinearen Gleichungssysteme:
1
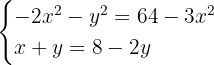
 ,
,
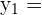
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
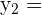
Dieses Feld ist erforderlich.
Wir vereinfachen soweit wie möglich:
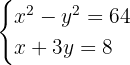
Wir lösen die 2. Gleichung nach  :
:

Wir setzen in die 1. Gleichung ein:

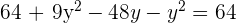
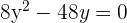
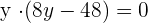
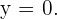
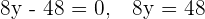

Wir setzen jeden Wert von  ein und erhalten die Werte von
ein und erhalten die Werte von  :
:


Die möglichen Lösungen sind:


2
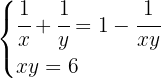
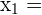
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
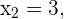
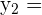
Dieses Feld ist erforderlich.
Wir lösen die 2. Gleichung nach  :
:
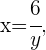
Wir setzen in die 1. Gleichung ein:

Wir führen die notwendigen Berechnungen durch:
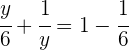

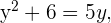
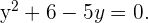
Wir lösen die quadratische Gleichung und erhalten:
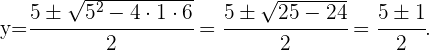
Somit lauten die Lösungen für
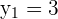 und
und 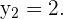
Für jeden Wert von  erhalten wir einen Wert von
erhalten wir einen Wert von  :
:

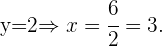
Die möglichen Lösungen sind:

3
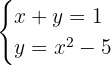
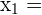
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
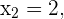
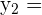
Dieses Feld ist erforderlich.
Wir lösen die 1. Gleichung nach  :
:

Wir setzen in die 2. Gleichung ein:



Die Lösungen für  sind
sind
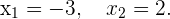
Nun lösen wir nach  und erhalten Folgendes, zunächst für y
und erhalten Folgendes, zunächst für y 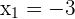

und für  erhalten wir
erhalten wir
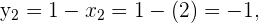
Somit lauten die Lösungen

4
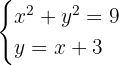

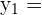
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
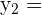
Dieses Feld ist erforderlich.
Wir setzen die 2. Gleichung in die 1. Gleichung ein
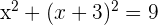

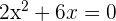

Also sind die Lösungen für 
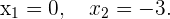
Nun lösen wir nach  , zunächst für
, zunächst für 
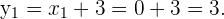
Und für 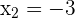
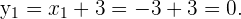
Die Lösungen sind
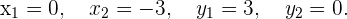
5
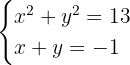
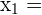
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
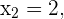
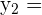
Dieses Feld ist erforderlich.
Wir lösen die 2. Gleichung nach  :
:
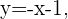
Wir setzen in die 1. Gleichung ein:
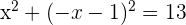
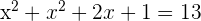



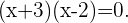
Somit sind die Lösungen für  gegeben durch
gegeben durch
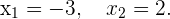
Nun lösen wir nach  , zunächst für
, zunächst für 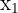

Nun für 
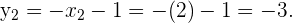
Die Lösungen sind

6
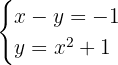
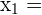
Dieses Feld ist erforderlich.
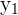
Dieses Feld ist erforderlich.
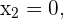

Dieses Feld ist erforderlich.
Zunächst lösen wir die 1. Gleichung nach 
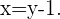
Dies setzen wir in die 2. Gleichung ein
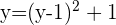
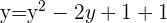
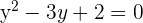
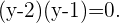
Somit sind die Lösungen für 

Nun suchen wir die Lösungen für  und beginnen hierfür mit
und beginnen hierfür mit 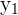
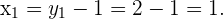
Und für  erhalten wir
erhalten wir

Die Lösungen sind

7
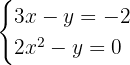
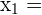
Dieses Feld ist erforderlich.

Dieses Feld ist erforderlich.
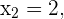
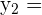
Dieses Feld ist erforderlich.
Zunächst lösen wir die 1. Gleichung nach  und erhalten
und erhalten
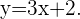
Nun setzen wir in die 2. Gleichung ein


Nun lösen wir die quadratische Gleichung
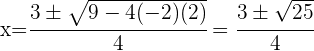
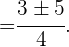
Somit lauten die Lösungen für 

Wir lösen nach  , zunächst mit
, zunächst mit 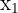
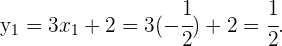
Für  erhalten wir
erhalten wir
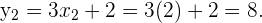
Die Lösungen des Systems sind

Mit KI zusammenfassen:


