Kapitel

Unvollständige quadratische Gleichungen
Gleichungen der Form 

1 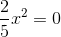
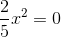
Um eine solche Gleichung zu lösen, kannst Du einfache Rechenschritte verwenden. Zuerst wandert die 5 durch Multiplikation auf die andere Seite, d.h.,
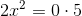
Daraus folgt:

Nun wandert die 2 durch Dividieren auf die andere Seite
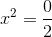
dann erhältst du die Gleichung
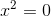
Die Lösung der quadratischen Gleichung ist also 0.
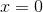
Quadratische Gleichungen mit unabhängigen Termen
Gleichungen der Form 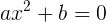
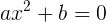
1 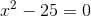

Entferne für eine solche Gleichung zunächst den quadratischen Term, d. h.,
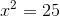
ziehe nun auf beiden Seiten die Quadratwurzel
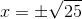
Die Lösungen sind daher:

2 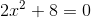

Entferne für eine solche Gleichung zunächst den quadratischen Term, d. h.,
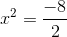
dann,
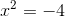
ziehe nun auf beiden Seiten die Quadratwurzel
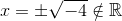
die Quadratwurzel aus einer negativen Zahl in den reellen Zahlen gibt es jedoch nicht. Daher hat die Gleichung keine reellen Wurzeln.
3 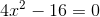
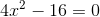
Entferne den quadratischen Term, um folgendes zu erhalten:
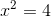
ziehe nun auf beiden Seiten die Quadratwurzel,
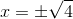
Die Lösungen sind daher:

4 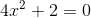
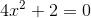
Entferne den quadratischen Term, um folgendes zu erhalten:
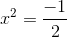
ziehe nun auf beiden Seiten die Quadratwurzel
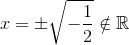
die Quadratwurzel aus einer negativen Zahl in den reellen Zahlen existiert jedoch nicht. Daher hat die Gleichung keine reellen Wurzeln.
Quadratische Gleichungen mit linearen Termen
Gleichungen der Form 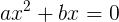
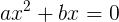
1 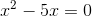
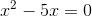
Nimm für eine solche Gleichung den gemeinsamen Faktor x heraus, d. h.
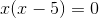
Da du ein Produkt gleich Null hast, ist entweder der eine Faktor Null oder der andere Faktor ist Null oder beide sind Null
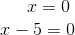
daher sind die Lösungen für die gegebene Gleichung 0 und 5

2 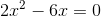
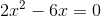
Nimm für eine solche Gleichung den gemeinsamen Faktor 2x heraus, d.h.
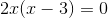
Da du ein Produkt gleich Null hast, ist entweder der eine Faktor Null oder der andere Faktor ist Null oder beide sind Null
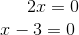
Daher sind die Lösungen der gegebenen Gleichung:

3 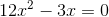
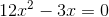
Vereinfache die Gleichung, indem du durch 3 dividierst und du erhältst:
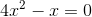
Nimm den gemeinsamen Faktor x heraus,
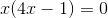
Da du ein Produkt gleich Null hast, ist entweder der eine Faktor Null oder der andere Faktor ist Null oder beide sind Null

Die Lösungen lauten daher:
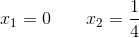
4 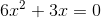
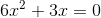
Nimm den gemeinsamen Faktor 3x heraus,
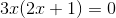
Da du ein Produkt gleich Null hast, ist entweder der eine Faktor Null oder der andere Faktor ist Null oder beide sind Null
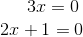
Die Lösungen lauten daher:
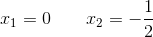
Mit KI zusammenfassen:













