Löse die folgenden Gleichungen:
1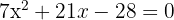 
2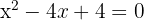 
3 
4 
1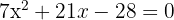
Sie kann mit der abc-Formel oder der Faktorisierungsmethode gelöst werden. Wende die Faktorisierungsmethode an:
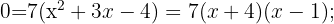
2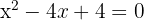
Wende die Faktorisierungsmethode an:
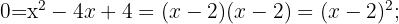
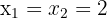
3
Wende die Faktorisierungsmethode an:
4
Wende die Faktorisierungsmethode an:
Löse die folgenden Gleichungen:
1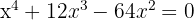 
2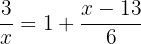 
1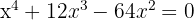
Wende die Faktorisierungsmethode an:
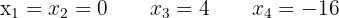
2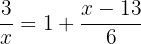
Vereinfache den Bruch auf der rechten Seite der Gleichung mit einem gemeinsamen Nenner und fasse dann die ganze Gleichung zusammen. Wende anschließend die Faktorisierungsmethode an:
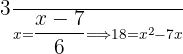
Löse die folgenden Gleichungen:
1 
2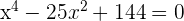 
1
Du kannst die Faktorisierungsmethode anwenden, zum Beispiel:
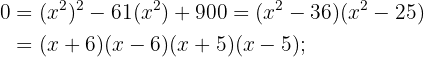
2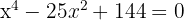 
Wende die Faktorisierungsmethode an:
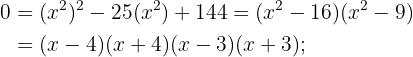
Löse die folgenden Gleichungen: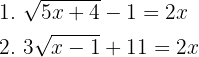
1 
Löse zuerst die Wurzel der Gleichung auf. Quadriere also beide Seiten der Gleichung und multipliziere die Klammer aus und löse die Gleichung.
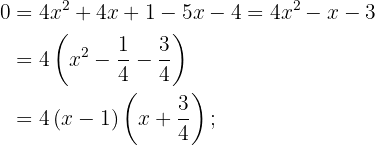
2 
Löse die Wurzel der Gleichung wird auf. Quadriere dann die beiden Seiten der Gleichung, fasse zusammen und löse mit der abc-Formel.
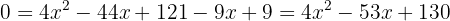
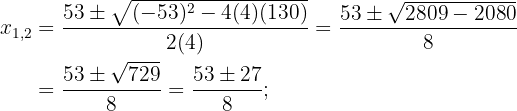
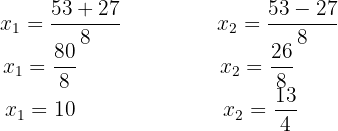
Finde die Wurzeln von: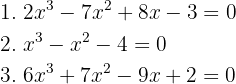
1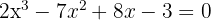 
Verwende die synthetische Division, weil die Gleichung dritten Grades ist. Die Teiler von 
sind also 
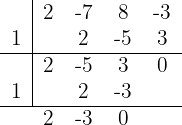
Dann ist die Faktorisierung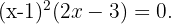 
Daher:
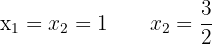
2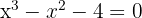 
Verwende die synthetische Division, weil die Gleichung dritten Grades ist. Die Teiler von 
sind also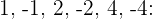 
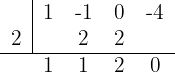
Dann lautet die Faktorisierung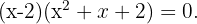 
Bei der Berechnung der Diskriminante des quadratischen Trinoms kannst Du feststellen, dass es keine Wurzeln hat, weil das Ergebnis negativ ist. Daher gibt es nur eine Lösung.
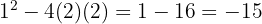
Verwende die synthetische Division, weil die Gleichung dritten Grades ist. Die Teiler von 
sind also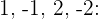 
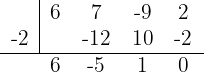
Dann lautet die Faktorisierung 
Löse die quadratische Gleichung mit der abc-Formel:
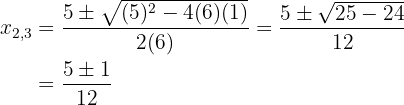
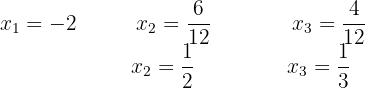
Löse die folgenden Gleichungssysteme: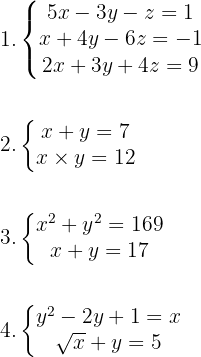 
1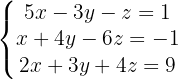 
Konstruiere die zum System gehörende Koeffizientenmatrix reduziere die Spalten und Zeilen.
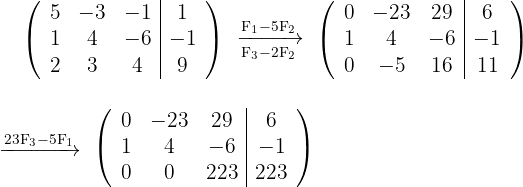
Es ergibt sich: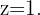 
Übertrage die letzte Matrix in das zugehörige Gleichungssystem, so hast du dann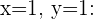 
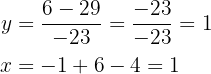
2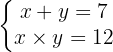 
Entferne eine Unbekannte aus der ersten Gleichung und setze das Resultat in die zweite Gleichung ein. Anschließend löst du die quadratische Gleichung.
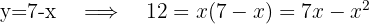
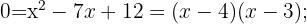
3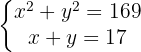 
Entferne eine Unbekannte aus der ersten Gleichung und setze das Resultat wird in die zweite Gleichung ein. Löse anschließend die quadratische Gleichung.
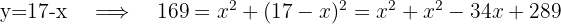
4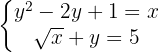 
Setze das Ergebnis für 
in die zweite Gleichung ein. Quadriere dann beide Teile der Gleichung und löse sie.
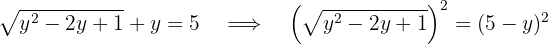
Bestimme den Wert von 
, damit die Lösungen der Gleichung 
den gleichen Wert haben.
Berechne die Diskriminante und setze sie auf Null. Somit ergibt sich eine Doppelwurzel.
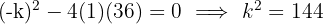
Die möglichen Werte für den Koeffizienten des linearen Terms sind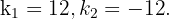 
Gesucht ist der Wert von zwei Zahlen, deren Summe fünf ist, und deren Produk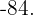t 
ist
Die Zahlenpaare sind 
y 
.
Bestimme das Alter von Peter: Du weißt, dass er in
Jahren die Hälfte des Quadrats des Alters sein wird, das er vor 
Jahren hatte.
Wenn für das aktuelle Alter steht, war er vor Jahren 
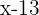Jahre alt und in Jahren wird er 
sein: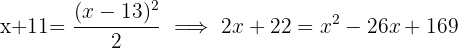
Daher ist Peter 
Jahre alt.
Zur Umzäunung eines rechteckigen Grundstücks von 
wurde ein Sichtschutznetz von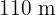 
verwendet. Berechne die Abmessungen des Grundstücks.
Dividiere das verwendete Sichtschutznetz durch zwei, so erhältst du den Halbperimeter des Grundstücks: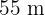 
. Daher kann das Problem mit den Formeln im Bild modelliert werden:
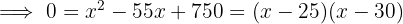
Das Grundstück hat Abmessungen von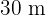 
und 
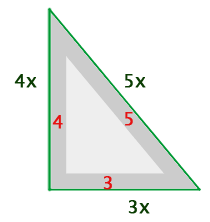
Die drei Seiten eines rechtwinkligen Dreiecks sind proportional zu den Zahlen 
Das Dreieck hat einen Flächeninhalt von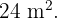 
Berechne die Länge jeder Seite des Dreiecks.
Die Seitenmaße des Dreiecks erhält man durch Multiplikation der Seiten des rechtwinkligen Dreiecks im Bild mit dem Faktor . Aus der Formel zur Berechnung der Fläche kann dieser Faktor bekannt sein.
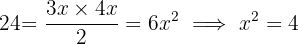
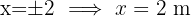
Die Seiten des Dreiecks sind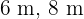 
y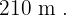 
Ein rechteckiger Garten mit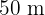 
Länge und 
Breite wird von einem Sandweg mit gleichmäßiger Breite umgeben. Berechnen Sie die Breite dieses Sandwegs, wenn er eine Fläche von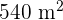 
hat.
Wenn du eine Breite des Sandwegs berücksichtigst, hast du ein größeres Rechteck mit den Abmessungen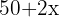 
por 
, wie in der Abbildung gezeigt. Nun wird die Fläche des Sandwegs mathematisch ausgedrückt.
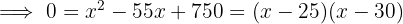
Daher ist der We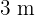g 
lang.
Berechne die Abmessungen eines Rechtecks, dessen Diagonale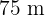 
misst, wobei Dir bekannt ist, dass es einem anderen Rechteck von 
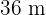auf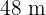 
ähnelt.
Da das Rechteck von 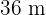auf 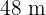dem Rechteck von 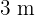auf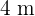 
ähnelt, wird auch das Rechteck, dessen Diagonale 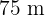misst, ähnlich sein. Es wird also angenommen, dass seine Seiten um den Faktor proportional sind, wie im Bild gezeigt. Der Satz des Pythagoras wird angewendet und der Wert der Unbekannten wird gefunden.
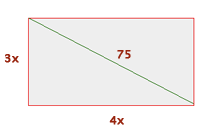
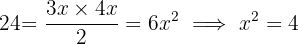
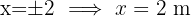
Daher ist das Rechteck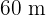 
lang und 
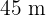breit.
Gesucht wird eine ganze Zahl, deren Summe mit dem Kehrwert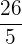 
ergibt.
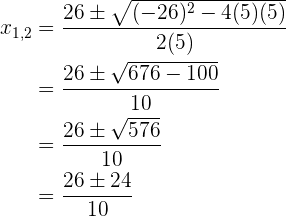
Die gesuchte Zahl ist fünf, weil die zweite Wurzel einen Bruch ergibt.
Berechne zwei natürliche Zahlen, deren Differenz zwei und die Summe ihrer Quadratzahlen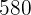 
ist.
Da die Differenz dieser Zahlen zwei ist, steht für eine Zahl und 
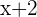für die zweite Zahl.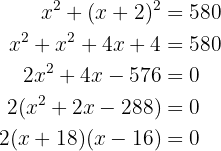
Die gesuchten Zahlen sind 
und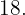 
Zwei Schläuche A und B füllen zusammen ein Schwimmbecken in zwei Stunden. A benötigt allein drei Stunden weniger als B. Berechnen Sie, wie viele Stunden jeder von ihnen braucht, um das Schwimmbecken zu füllen.
Wenn Schlauch A Stunden braucht, um den Pool zu füllen, braucht Schlauch B 
Stunden, um den Pool zu füllen. Somit wird jede Stunde A 
Teil des Schwimmbeckens füllen und B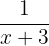 
partes. Teile. Da beide Schläuche gemeinsam das Schwimmbecken vollständig füllen, gilt: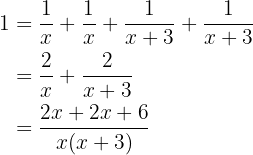
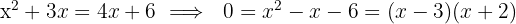
Schlauch A braucht 
Stunden, um das Schwimmbecken zu füllen, und Schlauch B braucht 
Stunden.
Gesucht sind zwei Zahlen, deren Produkt vier und die Summe ihrer Quadratzahlen siebzehn ist.
Stelle das Gleichungssystem mit zwei Unbekannten auf und löse es.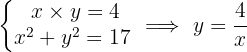
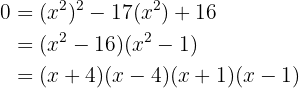
Die möglichen Zahlenpaare si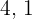nd 
und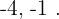 
Finde einen Bruch, der 
entspricht und dessen Quadratzahlen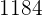 
ergeben.
Stelle das Gleichungssystem mit zwei Unbekannten auf und löse es.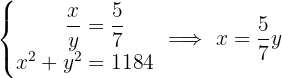
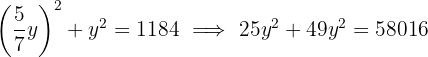
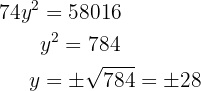
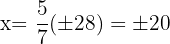
Der Bruch, der die Anforderung erfüllt, ist 
, da in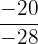 
die negativen Vorzeichen aufgehoben werden und der erste Bruch erhalten wird.
Ein Supermarktkunde hat insgesamt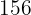 
für 
L Milch, kg Schinken und L Olivenöl bezahlt. Berechne den Preis der einzelnen Artikel. Du weißt, dass ein Liter Öl dreimal so viel kostet wie ein Liter Milch und dass ein Kilogramm Schinken dasselbe kostet wie der Kauf von 
L Öl plus L Milch.
Die Kosten für Milch, Schinken und Olivenöl sind jeweils mit 
gekennzeichnet. Stelle das zugehörige Gleichungssystem auf und löse es.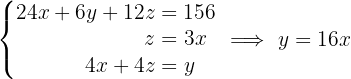
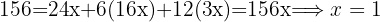
Milch kostet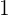 
pro Liter, Schinken 
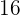pro Kilogramm und Olivenöl 
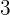pro Liter.
Eine Videothek ist auf drei Arten von Filmen spezialisiert: Kinderfilme, amerikanische Western und Horrorfilme. Es ist bekannt, dass:
der Kinderfilme plus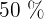 
der Western machen 
der Gesamtzahl der Filme aus.
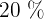der Kinderfilme plus der Western plus der Horrorfilme machen die Hälfte der Gesamtzahl der Filme aus.
Ermittle die Anzahl der Filme jedes Typs, wobei du weißt, dass es unter 
Filmen mehr Western als Kinderfilme gibt.
Kinderfilme, Western und Horrorfilme sind jeweils mit gekennzeichnet. Stelle das zugehörige Gleichungssystem auf und löse es.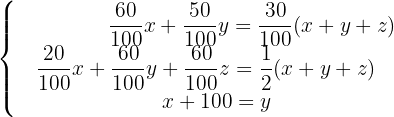
Vereinfache das Gleichungssystem und erhalte
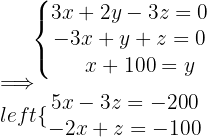
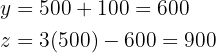
Die Videothek hat 
Kinderfilme, 
Western und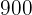 
Horrorfilme.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
