Kapitel
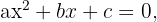mit 
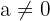
Die quadratische Gleichung wird durch Anwendung der folgenden Formel gelöst:
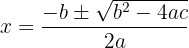
Beispiel: Finde die Lösungen von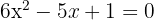 
1 Finde zuerst die Werte der Koeffizienten
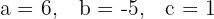
2 Setze dann die Werte in die Formel ein und löse die Gleichung
3 Du stellst fest, dass sich für 
, zwei Werte ergeben, die üblicherweise durch 
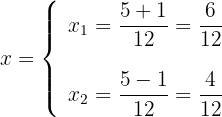
4 Vereinfache die Ergebnisse und du erhältst
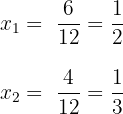
Diskriminante und Lösungsarten
Der Radikand der Quadratwurzel, den du in der Formel zur Lösung einer quadratischen Gleichung findest, wird als Diskriminante bezeichnet
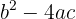
Aus der Diskriminante ist es möglich, die Art der Lösungen der quadratischen Gleichung zu erkennen
1 Wenn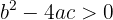 
, dann sind 
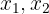reale und eindeutige Lösungen.
2 Wenn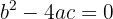 
, dann sind 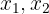reelle und gleiche Lösungen.
3 Wenn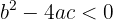 
, dann hat die Gleichung keine reellen Lösungen.
Beispiel: Bestimme die Arten von Lösungen für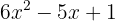 
Die Koeffizienten sind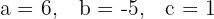
Setze die Werte in die Formel ein und löse die Gleichung
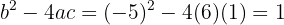
Da die Diskriminante größer als Null ist, hat die quadratische Gleichung zwei reelle und eindeutige Lösungen.
Übungen zu quadratischen Gleichungen aus deren Lösungen
Finde die quadratischen Gleichungen, die folgende Lösungen haben:
1
1Wenn du die Werte der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Wurzeln und du erhältst:
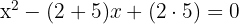
3Die gesuchte Gleichung lautet also:
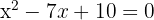
2
1Wenn du die Wurzeln der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Wurzeln und du erhältst:
3Die gesuchte Gleichung lautet also:
3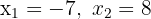
1Wenn du die Werte 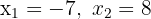der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Werte und du erhältst:
3Die gesuchte Gleichung lautet also:
4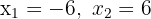
1Wenn du die Werte 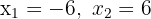der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Werte und du erhältst:
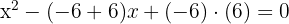
3Die gesuchte Gleichung lautet also:
5
1Wenn du die Wurzeln der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Werte und du erhältst:
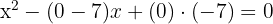
3Die gesuchte Gleichung lautet also:
6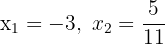
1Wenn du die Werte 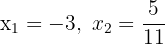der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Werte und du erhältst:
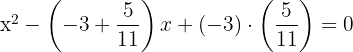
3Die gesuchte Gleichung lautet also:
4Die vorherige Gleichung kann mit ganzzahligen Koeffizienten ausgedrückt werden, dazu multiplizierst du beide Seiten der Gleichung mit 
7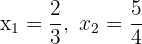
1Wenn du die Werte 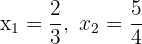der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituiere die Wurzeln und du erhältst:
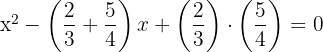
3Die gesuchte Gleichung lautet also:
4Die vorherige Gleichung kann mit ganzzahligen Koeffizienten ausgedrückt werden, dazu multiplizierst du beide Seiten der Gleichung mit 
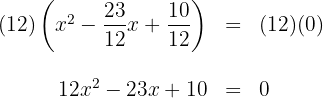
8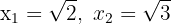
1Wenn du die Werte 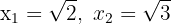der quadratischen Gleichung kennst, kannst du diese Gleichung folgendermaßen darstellen:
2Substituierst die Werte und du erhältst:
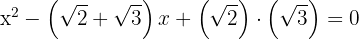
3Die gesuchte Gleichung lautet also:
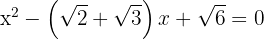
Faktorisierung von quadratischen Gleichungen: Aufgaben
Faktorisiere die folgenden quadratischen Gleichungen
1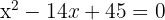
11 Die Koeffizienten der quadratischen Gleichung sind: 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
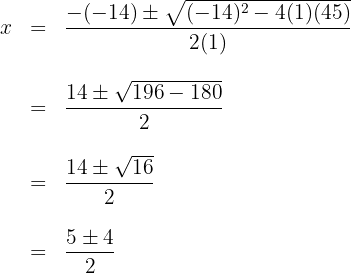
3 Du stellt fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden.
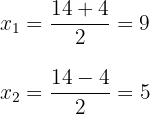
4 Die gesuchte Faktorisierung ist gegeben durch 
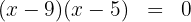
2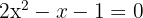
1Die Koeffizienten der quadratischen Gleichung sind: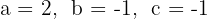 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
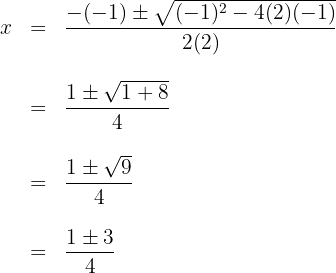
3 Du stellst fest, dass sich für , zwei Werte ergeben, die üblicherweise durch dargestellt werden.
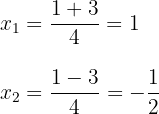
4 Die gesuchte Faktorisierung ist gegeben durch
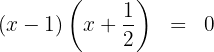
5 Du kannst die Faktoren mit ganzzahligen Koeffizienten erhalten, schreibe dazu den zweiten Faktor mit einem gemeinsamen Nenner und multipliziere dann beide Seiten der Gleichung mit diesem Nenner
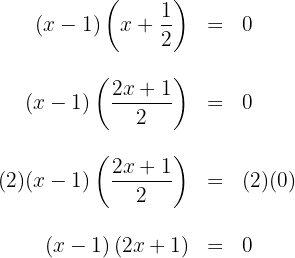
3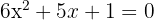
1Die Koeffizienten der quadratischen Gleichung sind: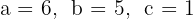 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
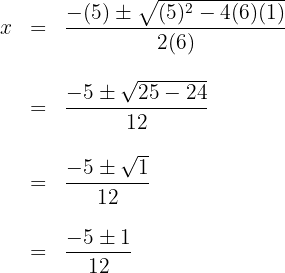
3 Du stellst fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden
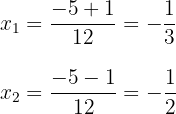
4 Die gesuchte Faktorisierung ist gegeben durch
5 Du kannst die Faktoren mit ganzzahligen Koeffizienten erhalten, schreibe dazu jeden Faktor mit einem gemeinsamen Nenner und multipliziere dann beide Seiten der Gleichung mit dem Produkt der beiden Nenner
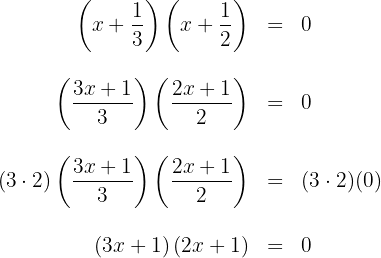
4
1 Die Koeffizienten der quadratischen Gleichung sind: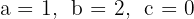 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
3 Du stellst fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden.
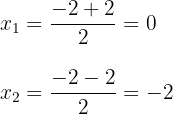
4 Die gesuchte Faktorisierung ist gegeben durch
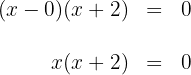
5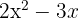
1Die Koeffizienten der quadratischen Gleichung sind: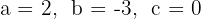 
.
2 Setzte die Werte in die Formel ein, um die Lösungen zu erhalten und löse
3 Du stellst fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden.
4 Die gesuchte Faktorisierung ist gegeben durch
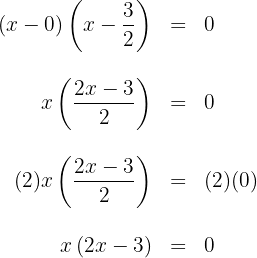
6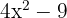
1Die Koeffizienten der quadratischen Gleichung sind: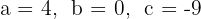 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
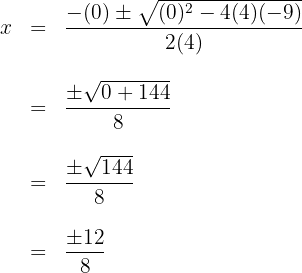
3 Du stellst fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden
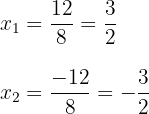
4 Die gesuchte Faktorisierung ist gegeben durch
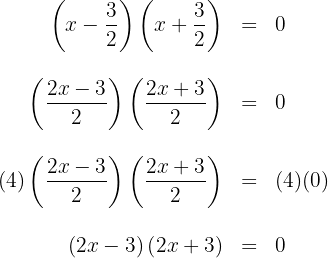
7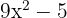
1Die Koeffizienten der quadratischen Gleichung sind: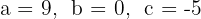 
.
2 Setze die Werte in die Formel ein, um die Lösungen zu erhalten und löse
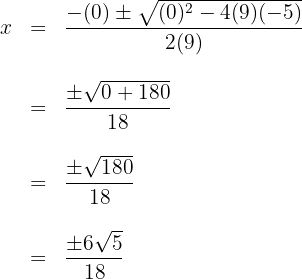
3 Du stellst fest, dass sich für zwei Werte ergeben, die üblicherweise durch dargestellt werden
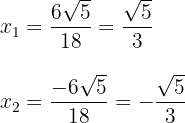
4 Die gesuchte Faktorisierung ist gegeben durch
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
