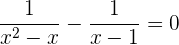
1 Berechne das kleinste gemeinsame Vielfache (kgV) der NennerBringe die Gleichung auf einen gemeinsamen Nenner, indem du das kgV der Nenner ermittelst: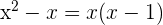
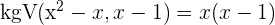
2 Du erhältst einen gleichwertigen, nicht rationalen Ausdruck
Teile das kgV durch den jeweiligen Nenner und multipliziere das Ergebnis mit dem Zähler.
Somit erhältst du:
3 Überprüfe die Lösung
Setze die erhaltene Lösung ein, um zu überprüfen, ob die Gleichung aufgeht:
Die Gleichung besitzt keine Lösung, da für x = 1 die Nenner aufgehoben werden.
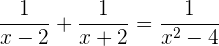
1 Berechne das kleinste gemeinsame Vielfache (kgV) der NennerBringe auf einen gemeinsamen Nenner, indem du das kgV der Nenner ermittelst:
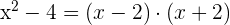
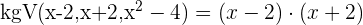
2 Du erhältst einen gleichwertigen, nicht rationalen Ausdruck
Teile das kgV durch den jeweiligen Nenner und multipliziere das Ergebnis mit dem Zähler.
Somit erhältst du:
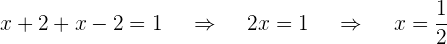
3Überprüfe die Lösung
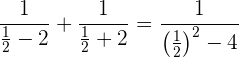
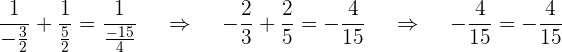
Die Lösung ist: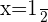 
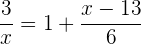
1 Berechne das kleinste gemeinsame Vielfache (kgV) der NennerBringe auf einen gemeinsamen Nenner, indem du das kgV der Nenner ermittelst:
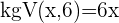
2 Du erhältst einen gleichwertigen, nicht rationalen Ausdruck
Teile das kgV durch den jeweiligen Nenner und multipliziere das Ergebnis mit dem Zähler.
Somit erhältst du:
Verwende die allgemeine Formel, um die quadratische Gleichung zu lösen:
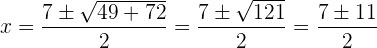
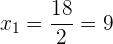
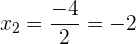
3Überprüfe die Lösung
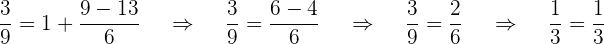
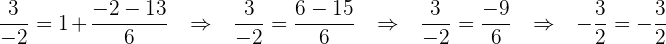
Finde eine ganze Zahl, deren Summe mit ihrer Inversen gleich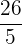 
ist
1 Stelle die Gleichung aufZahl: 
Inverse der Zahl: 
Summe der Zahl und ihrer Inversen: 
2Entferne die Nenner
Du erhältst eine rationale Gleichung und musst zuerst die Nenner entfernen:
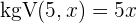
3Löse auf
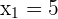
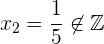
4 Überprüfe
Die gesuchte Zahl ist 5, aber da es keine rationale Gleichung ist, überprüfen wir noch einmal:
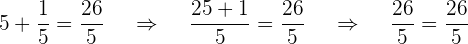
ist keine Lösung, da es sich nicht um eine ganze Zahl handelt
Ein Becken wird über zwei Rohre A und B innerhalb von zwei Stunden aufgefüllt. A würde drei Stunden weniger als B benötigen, um das Becken allein zu füllen. Wie viele Stunden braucht jedes Rohr für sich allein?
1 Stelle die Gleichung aufZeit, die A benötigt 
Zeit, die B benötigt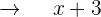 
Zeit von A und B zusammen 
Geschwindigkeit, mit der A das Becken füllt 
Geschwindigkeit, mit der B das Becken füllt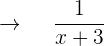 
Geschwindigkeit, mit der A und B das Becken füllen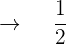 
Da A und B zusammen das Becken innerhalb von 2 Stunden füllen, summieren wir die Füllzeit von beiden und erhalten:
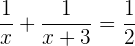
2 Entferne die Nenner
Du erhältst eine rationale Gleichung und musst zuerst die Nenner entfernen:
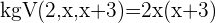
3 Löse auf
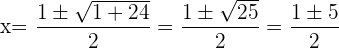
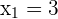
4 Überprüfe
Prüfe, ob 3 eine mögliche Lösung ist:
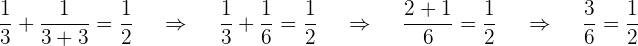
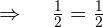
Zeit von A 3 Stunden
Zeit von B 6 Stunden
Über Rohr A wird ein Behälter zwei Stunden langsamer als über Rohr B befüllt. Wenn man beide Rohre öffnet, füllt sich der Behälter innerhalb von 1 Stunde und 20 Minuten. Wie lange benötigt jedes Rohr, um den Behälter alleine zu füllen?
1 Stelle die Gleichung aufStelle die Zeitangabe als Bruch dar
1 Stunde und 20 Minuten = 4/3 Stunden
Zeit von Rohr A x
Zeit von Rohr B x − 2
Zeit von beiden zusammen 
Geschwindigkeit von Rohr A
Geschwindigkeit von Rohr B 
Geschwindigkeit von beiden zusammen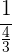 
Da das Becken mit beiden Rohren in Std. befüllt wird, bilden wir die Summe aus beiden Einzelfüllungen und erhalten:
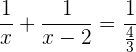
Bilde die Inverse auf der rechten Seite der Gleichung
2Entferne die Nenner
Das kgV ist 4x(x − 2)
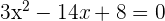
3Löse auf
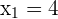
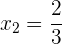
Zeit von Rohr A: 4 Stunden
Zeit von Rohr B: 2 Stunden
Wir sehen, dass 
keine Lösung sein kann, da die Zeit des zweiten Rohrs negativ wäre.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
