Ein Gleichungssystem ist nichtlinear, wenn mindestens eine seiner Gleichungen nicht vom ersten Grad ist.
Beispiel:
Schritte der Substitutionsmethode
Die Auflösung dieser Systeme erfolgt in der Regel durch die Substitutionsmethode, dazu werden die folgenden Schritte befolgt:
1Eliminiere eine Unbekannte in einer der Gleichungen, vorzugsweise in der linearen Gleichung.
2Setze den Wert der Unbekannten in die andere Gleichung.
3 Löse die resultierende Gleichung.
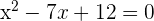
4 Setze jeden der erhaltenen Werte in die andere Gleichung ein und du erhältst die entsprechenden Werte der anderen Unbekannten.
Gleichungssysteme: Aufgaben mit Lösungen
1
2Setze sie in die andere Gleichung ein
Berechne
Du stellst fest, dass es sich um folgende quadratische Gleichung handelt:
3Löse auf
Durch die abc-Formel weißt du, dass
4Erhalte den Wert der anderen Unbekannten
2
2Setze sie in die andere Gleichung ein
Berechne
Du stellst, dass es sich um die folgende quadratische Gleichung handelt:
3Löse auf
Durch die abc-Formel weißt du, dass
4Erhalte den Wert der anderen Unbekannten
In diesem Fall gibt es keinen ersten Grad, aber wir stellen fest, dass x bereits in der ersten Gleichung eliminiert wurde.
2Setze sie in die andere Gleichung ein
Löse die Wurzel auf
Quadriere
Berechne
3Löse auf
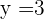
4Erhalte den Wert der anderen Unbekannten
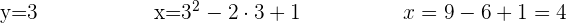
4 
stellst du fest, dass die ursprüngliche Gleichung folgendermaßen lauten würde:
2Eliminiere eine der Unbekannten aus einer der Gleichungen
3Setze sie in die andere Gleichung ein
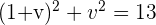
Berechne
4Löse auf
Dank der abc-Formel weißt du, dass
5Erhalte den Wert der anderen Unbekannten
5Schaue dir noch einmal die Änderung der Variablen an, die du zu Beginn vorgenommen hast
Mit der Lösung von 
Mit der Lösung von 
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
