
Aufgaben zu linearen Gleichungen
Löse folgende Gleichung:
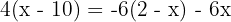
1 Auflösen der Klammern auf beiden Seiten der Gleichung durch Ausmultiplizieren

2 Wir fassen Terme durch Addition und Subtraktion auf beiden Seiten der Gleichung zusammen
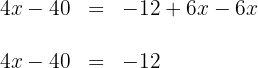
3 Um  zu bestimmen, addieren wir beide Seiten der Gleichung zunächst mit
zu bestimmen, addieren wir beide Seiten der Gleichung zunächst mit  und vereinfachen sie
und vereinfachen sie
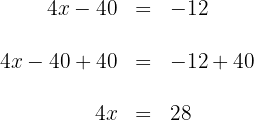
4 Um den Wert für  zu erhalten, multiplizieren wir jetzt beide Seiten der Gleichung mit
zu erhalten, multiplizieren wir jetzt beide Seiten der Gleichung mit  und vereinfachen sie
und vereinfachen sie
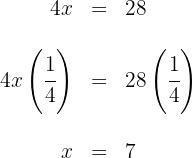
Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:

1 Ausmultiplizieren
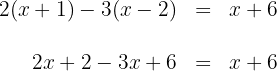
2 Wir fassen Terme durch Addition und Subtraktion auf beiden Seiten der Gleichung zusammen
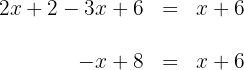
3 Um  zu bestimmen, substrahieren wir zunächst
zu bestimmen, substrahieren wir zunächst  und
und  auf beiden Seiten der Gleichung und vereinfachen sie
auf beiden Seiten der Gleichung und vereinfachen sie
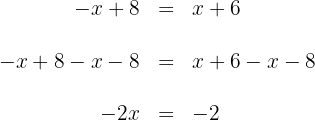
4 Um  zu bestimmen, multiplizieren wir jetzt beide Seiten der Gleichung mit
zu bestimmen, multiplizieren wir jetzt beide Seiten der Gleichung mit  und vereinfachen sie
und vereinfachen sie

Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:
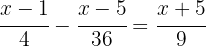
1 Wir berechnen das 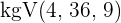
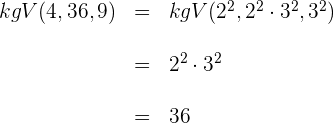
2 Wir multiplizieren beide Seiten der Gleichung mit dem 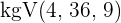
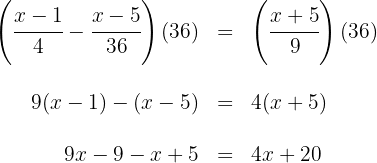
3 Wir fassen Terme durch Addition und Subtraktion auf beiden Seiten der Gleichung zusammen
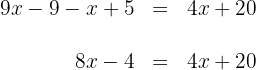
4 Um  zu bestimmen, subtrahieren wir zunächst
zu bestimmen, subtrahieren wir zunächst  und addieren
und addieren  auf beiden Seiten der Gleichung und vereinfachen sie
auf beiden Seiten der Gleichung und vereinfachen sie
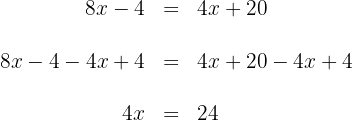
5 Um  zu bestimmen, multiplizieren wir jetzt beide Seiten der Gleichung mit
zu bestimmen, multiplizieren wir jetzt beide Seiten der Gleichung mit  und vereinfachen sie
und vereinfachen sie
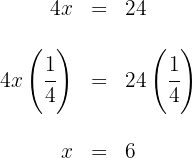
Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:
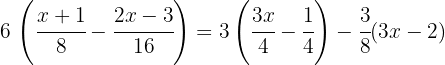
1 Brüche durch Ausmultiplizieren vereinfachen
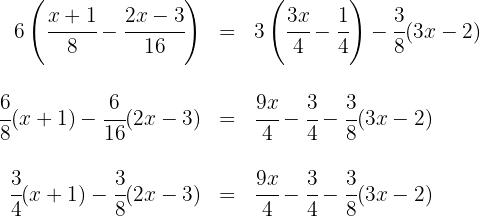
2 Wir berechnen das 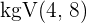 der Nenner
der Nenner
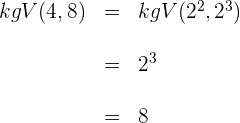
3 Wir multiplizieren beide Seiten der Gleichung mit dem 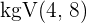
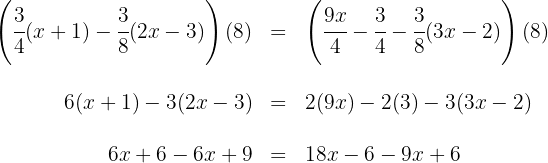
4 Wir addieren und subtrahieren auf beiden Seiten der Gleichung
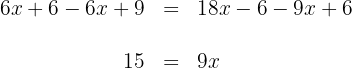
5 Um  zu bestimmen, multiplizieren wir beide Seiten der Gleichung mit
zu bestimmen, multiplizieren wir beide Seiten der Gleichung mit  und vereinfachen sie
und vereinfachen sie
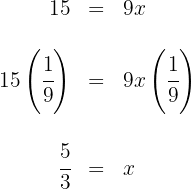
Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:

1 Wir multiplizieren beide Seiten der Gleichung mit  y
y  und vereinfachen sie
und vereinfachen sie
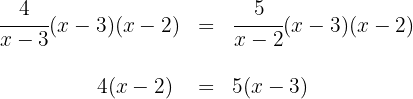
2 Ausmultiplizieren

3 Wir subtrahieren  und addieren
und addieren  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung
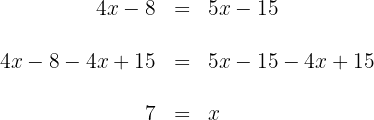
Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:
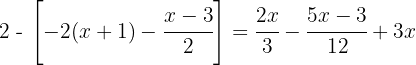
1 Wir lösen die eckigen Klammern auf

2 Wir berechnen das 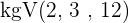 der Nenner
der Nenner
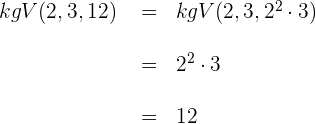
3 Wir multiplizieren beide Seiten der Gleichung mit dem 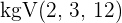

4 Wir addieren und subtrahieren
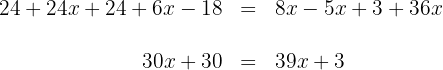
5 Wir subtrahieren 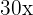 und
und  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung
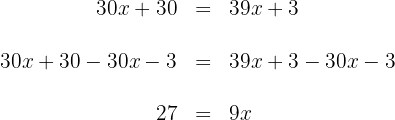
6 Wir multiplizieren beide Seiten der Gleichung mit 

Somit ist die Lösung der Gleichung 
Löse folgende Gleichung:
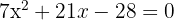
1 Um die Wurzeln der Gleichung zweiten Grades zu bestimmen, wenden wir die Formel an
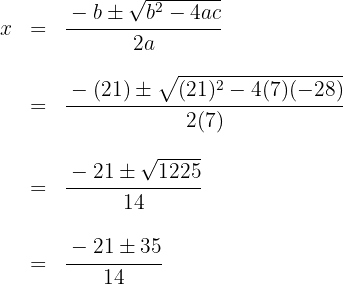
Somit ergibt sich
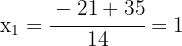
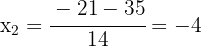
2 Durch die Wurzelrechnung erhalten wir  und
und 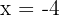 als Lösungen für die Gleichung
als Lösungen für die Gleichung
Löse folgende Gleichung:

1 Um die Wurzeln der Gleichung zweiten Grades zu bestimmen, wenden wir die Formel an

Da es nicht möglich ist, die Wurzel einer negativen Zahl zu bestimmen, kommen wir zu dem Schluss, dass die Gleichung keine Lösung hat
Löse folgende Gleichung:

1 Um die Wurzeln der Gleichung zweiten Grades zu bestimmen, wenden wir die Formel an
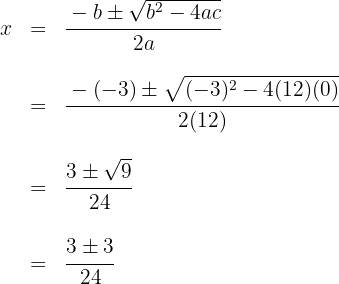
Somit ergibt sich
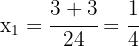
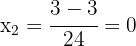
2 Durch die Wurzelrechnung erhalten wir  und
und  als Lösungen für die Gleichung
als Lösungen für die Gleichung
Löse folgende Gleichung:
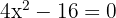
1 Um die Wurzeln der Gleichung zweiten Grades zu bestimmen, wenden wir die Formel an
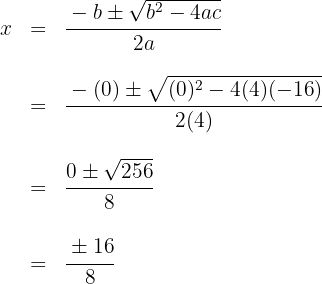
Somit ergibt sich
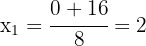
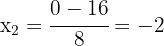
2 Durch die Wurzelrechnung erhalten wir  und
und  als Lösungen für die Gleichung
als Lösungen für die Gleichung
Anwendungsaufgaben
Ein Vater ist 35 Jahre alt, sein Sohn 5. In wie vielen Jahren ist der Vater genau dreimal so alt wie sein Sohn?
1 Der Vater ist 35 Jahre alt, sein Sohn 5.  steht für die Jahre, die vergehen müssen, bis die gegebene Bedingung erfüllt wird
steht für die Jahre, die vergehen müssen, bis die gegebene Bedingung erfüllt wird
2 Die Bedingung drücken wir in Form einer Gleichung aus
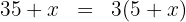
3 Ausmultiplizieren
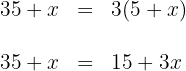
4 Wir subtrahieren  und
und  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung

5 Um  zu bestimmen, multiplizieren wir beide Seiten der Gleichung mit
zu bestimmen, multiplizieren wir beide Seiten der Gleichung mit  und vereinfachen sie
und vereinfachen sie
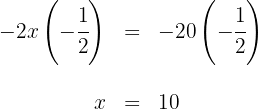
6 In  Jahren ist der Vater genau dreimal so alt wie sein Sohn.
Jahren ist der Vater genau dreimal so alt wie sein Sohn.
Wenn man vom doppelten Wert einer Zahl die Hälfte subtrahiert, ist das Ergebnis 54. Was ist die gesuchte Zahl?
1 Da wir die gesuchte Zahl nicht kennen, benennen wir sie mit 
2 Die Bedingung drücken wir in Form einer Gleichung aus
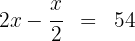
3 Ausmultiplizieren auf beiden Seiten der Gleichung
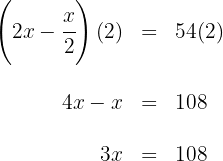
4 Wir multiplizieren beide Seiten der Gleichung mit 
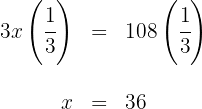
5 Die gesuchte Zahl ist 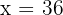
Ein Rechteck ist doppelt so breit wie hoch. Was sind die Maße des Rechtecks, wenn sein Umfang 30 cm beträgt?
1 Die Höhe des Rechtecks stellen wir mit  dar. Daraus ergibt sich eine Breite von
dar. Daraus ergibt sich eine Breite von 
2 Für den Umfang stellen wir eine Gleichung auf

3 Ausmultiplizieren und addieren

4 Wir multiplizieren beide Seiten der Gleichung mit 
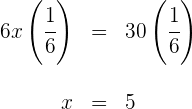
5 Für die Höhe gilt 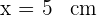 und für die Breite gilt
und für die Breite gilt 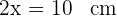
Auf einer Feier sind doppelt so viele Frauen wie Männer und dreimal so viele Kinder wie Männer und Frauen zusammen. Wie viele Männer, Frauen und Kinder sind auf der Feier anwesend, wenn insgesamt 96 Personen teilnehmen?
1 Die Anzahl der Männer stellen wir mit  dar, daraus ergibt sich die Anzahl der Frauen mit
dar, daraus ergibt sich die Anzahl der Frauen mit  und die Anzahl der Kinder mit
und die Anzahl der Kinder mit 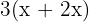
2 Die Bedingung drücken wir in Form einer Gleichung aus
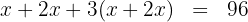
3 Ausmultiplizieren und addieren
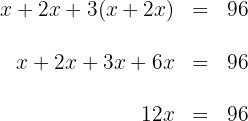
4 Wir multiplizieren beide Seiten der Gleichung mit 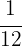
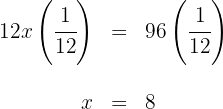
5 Die Anzahl der Männer beträgt  , die Anzahl der Frauen
, die Anzahl der Frauen 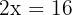 und die der Kinder
und die der Kinder 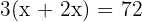
Von einem Ölkannister wurden  verbraucht.
verbraucht. 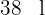 wurden wieder aufgefüllt und der Kannister ist nun zu
wurden wieder aufgefüllt und der Kannister ist nun zu  voll. Berechne das Fassungsvermögen des Kannisters.
voll. Berechne das Fassungsvermögen des Kannisters.
1 Das Fassungsvermögen benennen wir mit  und da
und da  seinen Fassungsvermögens verbraucht wurden, bleibt
seinen Fassungsvermögens verbraucht wurden, bleibt
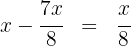
2 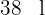 werden wieder aufgefüllt und wir stellen die zweite Bedingung in Form einer Gleichung dar
werden wieder aufgefüllt und wir stellen die zweite Bedingung in Form einer Gleichung dar

3 Wir multiplizieren beide Seiten der Gleichung mit dem 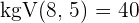

4 Wir subtrahieren 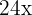 und
und  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung
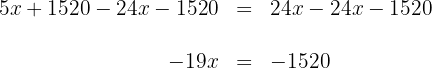
5 Wir multiplizieren beide Seiten der Gleichung mit 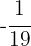

6 Der Kannister hat ein Fassungsvermögen von 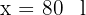
Auf einem Bauernhof leben Schweine und Puten. Insgesamt gibt es 35 Köpfe und 116 Beine. Wie viele Schweine und Puten gibt es dort?
1 Die Anzahl der Köpfe der Schweine benennen wir mit  und da es insgesamt 35 Köpfe gibt, ergibt sich somit für die Anzahl der Köpfe der Puten
und da es insgesamt 35 Köpfe gibt, ergibt sich somit für die Anzahl der Köpfe der Puten 
2 Nun legen wir die Bedingung für die Anzahl der Beine fest. Dabei ist zu beachten, dass Schweine 4 Beine haben, Puten 2.

3 Wir multiplizieren und addieren

4 Wir subtrahieren  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung
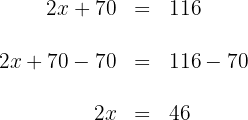
5 Wir multiplizieren beide Seiten der Gleichung mit 

6 Die Anzahl der Schweine beträgt 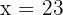 und die Anzahl der Puten beträgt
und die Anzahl der Puten beträgt 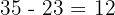 .
.
Luis macht eine Reise mit dem Auto, das dabei 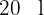 Benzin verbraucht. Die Strecke legt er in zwei Abschnitten zurück: Beim ersten verbraucht das Auto
Benzin verbraucht. Die Strecke legt er in zwei Abschnitten zurück: Beim ersten verbraucht das Auto  des Benzins, das noch im Tank war. Beim zweiten Abschnitt verbaucht das Auto die Hälfte des noch übrig gebliebenen Benzins. Wie viele Liter Benzin waren im Tank und wie viele Liter Benzin werden auf jedem Abschnitt der Strecke verbraucht?
des Benzins, das noch im Tank war. Beim zweiten Abschnitt verbaucht das Auto die Hälfte des noch übrig gebliebenen Benzins. Wie viele Liter Benzin waren im Tank und wie viele Liter Benzin werden auf jedem Abschnitt der Strecke verbraucht?
1 Die Anzahl der Liter Benzin im Tank benennen wir mit 
2 Für den ersten Streckenabschnitt legen wir fest 
3 Für den zweiten Streckenabschnitt legen wir fest

4 Um die Menge an Benzin, das im Tank war, zu bestimmen, addieren wir den Verbrauch beider Streckenabschnitte. Dieser liegt ingesamt bei 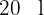
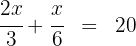
5 Wir multiplizieren beide Seiten der Gleichung mit 
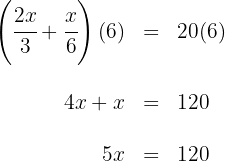
6 Wir multiplizieren beide Seiten der Gleichung mit 
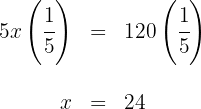
Somit ergibt sich, dass  im Tank waren
im Tank waren
Auf dem ersten Abschnitt verbraucht das Auto  , auf dem zweiten Abschnitt
, auf dem zweiten Abschnitt 
Anna geht in einen Buchladen und kauft mit einem Drittel ihres Geldes ein Buch und einen Comic mit den übrigen zwei Dritteln ihres Geldes. Anna bleiben dann noch 12€. Wie viel Geld hatte Anna am Anfang?
1 Den Gesamtbetrag benennen wir mit 
2 Für das Buch legen wir fest

3 Für den Comic legen wir fest
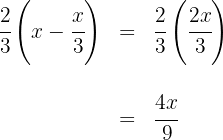
4 Um Annas Anfangsbetrag zu berechnen, addieren wir die Ausgaben für das Buch und den Comic mit dem Betrag, der ihr noch übrig bleibt.

5 Wir multiplizieren beide Seiten der Gleichung mit  und fassen zusammen
und fassen zusammen
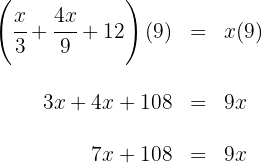
6 Wir subtrahieren 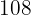 und
und 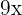 auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung
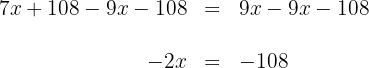
7 Wir multiplizieren beide Seiten der Gleichung mit 
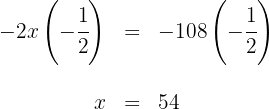
Somit hatte Anna am Anfang  €
€
Ein LKW verlässt eine Stadt mit 40 km/h. Eine Stunde später verlässt ein PKW mit 60 km/h diese Stadt und fährt in die selbe Richtung wie der LKW. An welchem Zeitpunkt holt der PKW den LKW ein?
1 Die Zeit, die der LKW benötigt, benennen wir mit  . Die Zeit für das Auto benennen wir mit
. Die Zeit für das Auto benennen wir mit 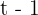
2 Beide Fahrzeuge legen die selbe Strecke zurück, deshalb gilt
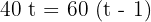
3 Ausmultiplizieren

4 Wir subtrahieren  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung

5 Wir multiplizieren beide Seiten der Gleichung mit 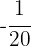
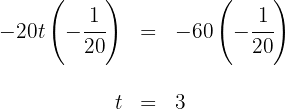
Somit dauert es für den LKW  , bis ihn das Auto einholt. Für das Auto dauert es
, bis ihn das Auto einholt. Für das Auto dauert es  , bis es den LKW einholt.
, bis es den LKW einholt.
Eine Zahl besteht aus zwei aufeinanderfolgenden Ziffern. Die größere Ziffer ist den Zehnern zuzuordnen, die kleinere Ziffer den Einern. Die Zahl entspricht der Summe der Ziffern, multipliziert mit sechs. Wie lautet die Zahl?
1 Die Ziffer aus den Einern benennen wir mit  . Da es sich um zwei aufeinanderfolgende Ziffern handelt, entspricht die Ziffer aus den Zehnern
. Da es sich um zwei aufeinanderfolgende Ziffern handelt, entspricht die Ziffer aus den Zehnern 
2 Wenn wir eine Zahl haben, die aus zwei Ziffern besteht, zum Beispiel  , können wir diese wie folgt zerlegen:
, können wir diese wie folgt zerlegen:
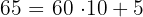
3 Unsere Zahl aus zwei Ziffern entspricht  , womit sich ergibt
, womit sich ergibt
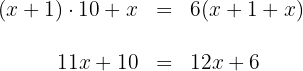
4 Wir subtrahieren 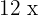 und
und  auf beiden Seiten der Gleichung
auf beiden Seiten der Gleichung

5 Wir multiplizieren beide Seiten der Gleichung mit  und erhalten
und erhalten 
6 Somit ist die gesuchte Zahl
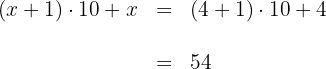
Mit KI zusammenfassen:













