
Begriff der unvollständigen quadratischen Gleichung
Wir sehen uns zunächst die vollständige quadratische Gleichung an, also die allgemeine Form der quadratischen Gleichung. So können wir im Folgenden besser verstehen, wann eine quadratische Gleichung unvollständig ist.
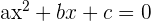
Eine quadratische Gleichung ist unvollständig, wenn einer der Koeffizienten: b oder c, oder beide, null sind. Daher gibt es in diesem Fall drei Arten von unvollständigen quadratischen Gleichungen.
Erster Fall
Wenn beide Koeffizienten null sind, sieht die unvollständige quadratische Gleichung wie folgt aus:
Wenn b=0 und c=0 , gilt ax² = 0 (unvollständige Gleichung 2. Grades).
Für diese Arte der Gleichung ist die Lösung immer x = 0.
Beispiele für den ersten Fall:
1 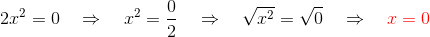
2 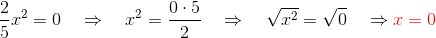
Zweiter Fall
Wenn der Koeffizient c null ist, sieht die unvollständige quadratische Gleichung wie folgt aus:
Wenn c=0 , gilt ax² + bx = 0 (unvollständige Gleichung 2. Grades).
Nun sehen wir uns an, wie wir die Lösungen ermitteln können:
1 Wir klammern den gemeinsamen Faktor x aus.
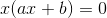
2 Da das Produkt gleich null ist, ist entweder ein Faktor gleich null oder der andere Faktor gleich null oder beide sind gleich null.
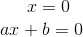
3 Die Lösungen sind also:
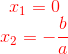
Beispiele für den zweiten Fall
1 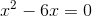
Wir klammern den gemeinsamen Faktor x aus.
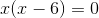
Da wir ein Produkt gleich null haben, setzen wir die Faktoren gleich null.
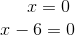
Die Lösungen sind:

2 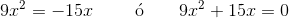
Wir klammern den gemeinsamen Faktor 3x aus.
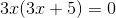
Da wir ein Produkt gleich null haben, setzen wir die Faktoren gleich null.
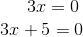
Die Lösungen sind:
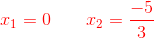
Dritter Fall
Wenn der Koeffizient b null ist, sieht die unvollständige quadratische Gleichung wie folgt aus:
Wenn b=0 , gilt ax² + c = 0 (unvollständige Gleichung 2. Grades).
Nun sehen wir uns an, wie wir die Lösungen ermitteln können:
1 Wir bringen den Term c auf die andere Seite, das Vorzeichen wechselt.
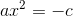
2 Wir bringen den Koeffizienten durch Division auf die andere Seite.
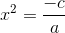
3 Auf beiden Seiten der Gleichung wird die Quadratwurzel gezogen und wir erhalten eine positive und eine negative Lösung:
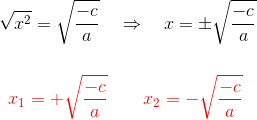
Beispiele für den dritten Fall
1 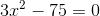
Wir bringen den Term c auf die andere Seite, das Vorzeichen wechselt.
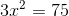
Wir bringen den Koeffizienten durch Division auf die andere Seite.
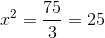
Auf beiden Seiten der Gleichung wird die Quadratwurzel gezogen und wir erhalten eine positive und eine negative Lösung:
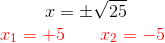
2 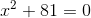
Wir bringen den Term c auf die andere Seite, das Vorzeichen wechselt.
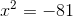
Wir bringen den Koeffizienten a durch Division auf die andere Seite. Da er 1 ist, ist das Ergebnis dasselbe wie im vorherigen Schritt.
Auf beiden Seiten der Gleichung wird die Quadratwurzel gezogen und wir erhalten einen negativen Radikanden, der keine reelle Zahl als Lösung hat.
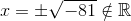
Mit KI zusammenfassen:













