Löse die folgenden Probleme:
1Ein Wasserhahn 
benötigt doppelt so viel Zeit wie ein weiterer Hahn 
, um einen Wassertank zu füllen und zusammen benötigen sie 
Minuten. Kannst du sagen, wie lange jeder der Wasserhähne braucht, um den Tank zu füllen, von dem wir sprechen?
Grifo 
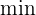
Dieses Feld ist erforderlich.
Hahn 
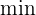
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall nicht wissen, wie lange jeder Wasserhahn zum Befüllen des Tanks benötigt, ist dies die Unbekannte in der von uns aufgestellten Gleichung
Der Hahn benötigt 
Stunden, um den Tank zu füllen.
Der Hahn benötigt 
Stunden, um den Tank zu füllen.
2 Die von jedem Wasserhahn innerhalb einer Stunde gefüllte Menge beträgt
In einer Stunde füllt Hahn 
des Tanks.
In einer Stunde füllt Hahn 
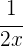des Tanks.
3 Wir wissen, dass die beiden Wasserhähne zusammen eine halbe Stunde brauchen, um den Tank zu füllen, also füllen sie zusammen in einer Stunde zwei Tanks
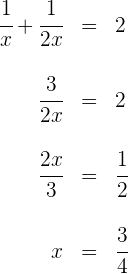
4 Somit benötigt der Wasserhahn eine Dreiviertelstunde, um den Tank zu füllen, d. h. 
Minuten. Andererseits benötigt der Wasserhahn 
Minuten, um den Tank zu füllen, d. h. 
Stunde und Minuten.
2Ein Wasserhahn benötigt dreimal so viel Zeit wie ein anderer Wasserhahn , um einen Wassertank zu füllen. Beide zusammen benötigen Minuten. Kannst du sagen, wie lange jeder der Wasserhähne braucht, um den Tank zu füllen, von dem wir sprechen?
Wasserhahn
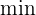
Dieses Feld ist erforderlich.
Wasserhahn
Du bist auf der Suche nach Nachhilfe in Mathe? Schau mal hier rein!
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall nicht wissen, wie lange jeder Wasserhahn zum Befüllen des Tanks benötigt, ist dies die Unbekannte in der von uns aufgestellten Gleichung.
Der Wasserhahn benötigt Stunden, um den Tank zu füllen.
Der Wasserhahn benötigt 
Stunden, um den Tank zu füllen.
2 Die von jedem Wasserhahn innerhalb einer Stunde gefüllte Menge beträgt
In einer Stunde füllt der Wasserhahn des Tanks.
In einer Stunde füllt der Wasserhahn 
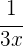des Tanks.
3 Wir wissen, dass die beiden Wasserhähne zusammen 30 Minuten brauchen, um den Tank zu füllen, also füllen sie zusammen in einer Stunde zwei Tanks
4 Somit benötigt der Wasserhahn zwei Drittel einer Stunde, um den Tank zu füllen, d. h. 
Minuten. Andererseits benötigt der Wasserhahn 
Minuten, um den Tank zu füllen, d. h. 
Stunden.
3Ein Wasserhahn benötigt 
Minuten, um einen Tank zu füllen und ein anderer Wasserhahn benötigt Minuten um denselben Tank zu füllen. Wie lange brauchen beide Wasserhähne, um den Tank zu füllen?
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall wissen, wie lange jeder Wasserhahn zum Befüllen des Tanks benötigt, haben wir:
Der Hahn befüllt in einer Minute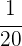 
des Tanks.
Der Hahn befüllt in einer Minute 
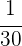des Tanks.
2 Die Zeit, die beide Wasserhähne zum Befüllen des Tanks benötigen, beträgt Minuten
In einer Minute füllen beide Wasserhähne des Tanks, also gilt
3 Somit benötigen beide Wasserhähne 
Minuten, um den Tank vollständig zu füllen
4Ein Wasserhahn benötigt Minuten, um einen Tank zu füllen und ein Ablasshahn benötigt Minuten, um denselben Tank zu leeren. Wie lange dauert es, bis sich der Tank bei gleichzeitig geöffnetem Wasserhahn und Ablasshahn füllt?
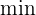
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall wissen, wie lange der Wasserhahn braucht, um den Tank zu füllen, und wie lange der Ablasshahn braucht, um ihn zu leeren, haben wir
Der Hahn befüllt in einer Minute 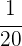des Tanks.
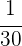Der Ablasshahn leer in einer Minute des Tanks.
2 Die Zeit, die beide Hähne zum Befüllen des Tanks benötigen, beträgt Minuten.
In einer Minute werden bei beiden offenen Hähnen des Tanks gefüllt, sodass gilt
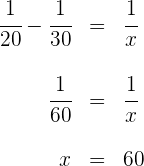
3 Wenn also beide Hähne geöffnet sind, dauert es 
Minuten, bis der Tank vollständig gefüllt ist.
5Wir wissen, dass ein Hahn doppelt so lange braucht wie ein anderer , um einen Tank mit Wasser zu füllen, und dass ein dritter Hahn 
dreimal so lange braucht wie , um denselben Tank zu füllen. Gib die Zeit an, die jeder der Wasserhähne benötigt, um den Tank zu füllen, wenn bekannt ist, dass sie zusammen Minuten benötigen, um ihn zu füllen.
Hahn
Dieses Feld ist erforderlich.
Hahn
Dieses Feld ist erforderlich.
Hahn
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall nicht wissen, wie lange jeder Wasserhahn zum Befüllen des Tanks benötigt, ist dies die Unbekannte in der von uns aufgestellten Gleichung.
Der Hahn benötigt Stunden, um den Tank zu füllen.
Der Hahn benötigt Stunden, um den Tank zu füllen.
Der Hahn benötigt Stunden, um den Tank zu füllen.
2 Die von jedem Wasserhahn innerhalb einer Stunde gefüllte Menge beträgt
In einer Stunde füllt der Wasserhahn des Tanks.
In einer Stunde füllt der Wasserhahn 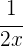des Tanks.
In einer Stunde füllt der Wasserhahn 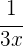des Tanks.
3 Wir wissen, dass die drei Wasserhähne zusammen eine halbe Stunde brauchen, um den Tank zu füllen, also füllen sie zusammen in einer Stunde zwei Tanks.
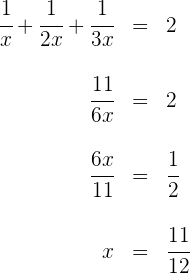
4 Somit benötigt der Wasserhahn elf Zwölftel einer Stunde, um den Tank zu füllen, d. h. 
Minuten. Andererseits benötigt der Wasserhahn 
Minuten, um den Tank zu füllen, d. h. Stunde und 
Minuten. Schließlich benötigt der Wasserhahn 
Minuten, um den Tank zu füllen, d. h. Stunden und Minuten.
6Wir wissen, dass ein Wasserhahn doppelt so lange braucht wie ein anderer Hahn , um einen Tank mit Wasser zu füllen, und dass ein Ablasshahn dreimal so lange braucht wie , um denselben Tank zu leeren. Gib die Zeit an, die jeder Wasserhahn benötigt, um den Tank zu füllen, und die Zeit, die der Ablasshahn benötigt, um ihn zu leeren, wenn bekannt ist, dass es bei drei geöffneten Hähnen Minuten dauert, ihn zu füllen.
Hahn
Dieses Feld ist erforderlich.
Hahn
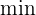
Dieses Feld ist erforderlich.
Ablasshahn
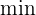
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall nicht wissen, wie lange jeder Hahn braucht, um den Tank zu füllen, wissen wir auch nicht, wie lange der Ablasshahn braucht, um ihn zu leeren. Dies ist also die Unbekannte in der Gleichung, die wir aufstellen.
Der Hahn benötigt Stunden, um den Tank zu füllen.
Der Hahn benötigt Stunden, um den Tank zu füllen.
Der Ablasshahn benötigt Stunden, um den Tank zu leeren.
2 Die von jedem Wasserhahn innerhalb einer Stunde gefüllte Menge beträgt
In einer Stunde füllt Hahn des Tanks.
In einer Stunde füllt Hahn 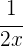des Tanks.
3 Die Menge des Wassers, die innerhalb einer Stunde durch den Ablasshahn fließt, beträgt
In einer Stunde füllt 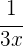des Tanks.
4 Wir wissen, dass die drei Hähne zusammen eine halbe Stunde brauchen, um den Tank zu füllen, also füllen sie zusammen in einer Stunde zwei Tanks
4 Somit benötigt der Wasserhahn sieben Zwölftel einer Stunde, um den Tank zu füllen, d. h. 
Minuten. Andererseits benötigt der Wasserhahn 
Minuten, um den Tank zu füllen, d. h. Stunde und 
Minuten. Schließlich dauert es 
Minuten, bis der Ablasshahn den Tank geleert hat, d. h. Stunde und Minuten.
7Wir möchten einen Pool mit zwei Wasserhähnen füllen. Hahn benötigt 
Stunden und Hahn benötigt 
Stunden. Wir wissen, dass der Pool ein Loch hat, durch das er in Stunden leer läuft. Wie lange brauchen die beiden Wasserhähne zusammen, um den Pool zu füllen?
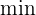
Dieses Feld ist erforderlich.
1 Da wir in diesem Fall wissen, wie lange die Wasserhähne brauchen, um den Tank zu füllen, und wie lange es dauert, bis er durch das Loch leer wird, gilt
Hahn füllt in einer Stunde 
des Pools.
Hahn füllt in einer Stunde 
des Pools.
Durch das Loch werden in einer Stunde agujero en una hora vacía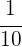 
des Pools geleert.
2 Die Zeit, die beide Wasserhähne zum Befüllen des Pools benötigen, beträgt Stunden
In einer Stunde, in der beide Wasserhähne geöffnet sind, füllen sich des Pools, sodass gilt:
3 Wenn also beide Wasserhähne geöffnet sind, dauert es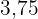 
Stunden, bis der Tank vollständig gefüllt ist, d. h. 
Stunden und Minuten.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
